文章 自习人课堂六西格玛学员笔记手稿

@牛马小白菜自习人课堂学习氛围浓厚学员彼此相互交流帮助晚上12点都在讨论学习六西格玛例如：需要相关资料，想进学习交流群，学习计划，备考攻略，项目辅导等扫码添加客服免费领取更多六西格玛绿带/黑带/质量经 理/可靠性工程师/ASQCSSBB/注册计量师相关资料在微信公众号：“自习人课堂”每一题都有详细解析思路与步骤的专业题库...

六西格玛

赞同0  578浏览  0评论 六六老师 2024-11-01 09:47

文章 中心点的加入会使得二水平变为三水平吗？

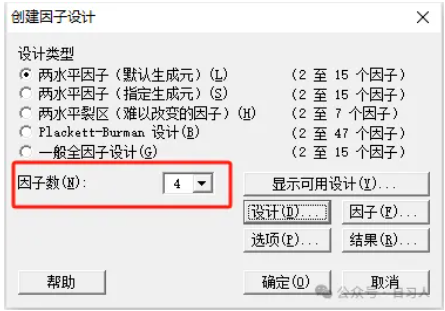
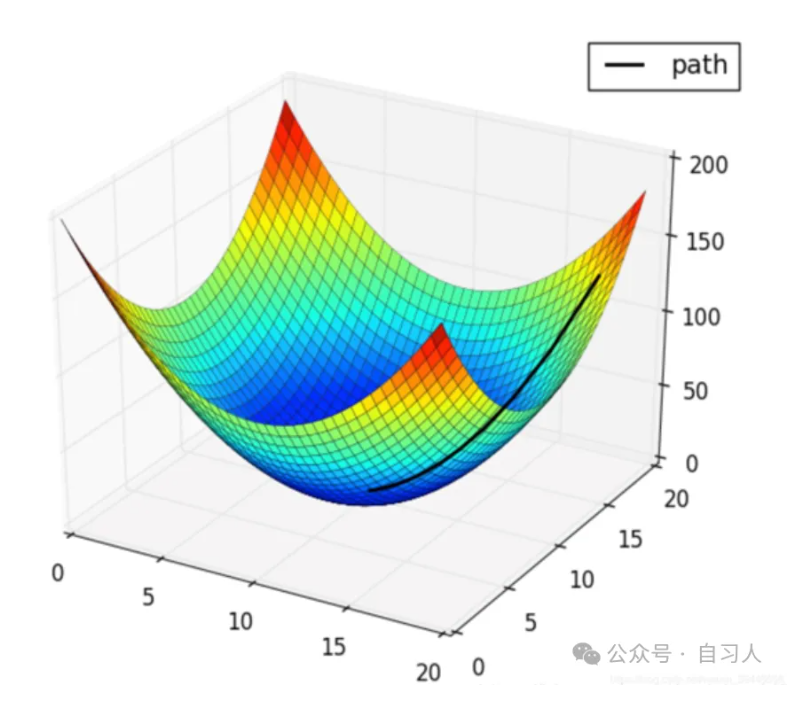
我们常说的加入中心点。重复试验和中心点都可以估计纯误差（这是考点）加入中心点有以下四大好处：第一：为了进行完全相同条件下的重复，因而可以估计出试验误差即随机误差。举个例子高水平是30g，低水平是10g ，在相同的条件下把中心点20g做三次试验得出数据，最终得到了中心点这三次的测量值，就可以计算出纯误差。第二：由于每个连续因子的取值原来只有两个值(高水平及低水平),现在增加到了三个值，因而增加了对于响 应变量可能存在的弯曲趋势估计的能力，这也是简单全面重复所不能达到的效果。第三：在把因子点试验的顺序随机化之后，如果再把在中心点处所进行的三次或四次试验安排在全部试验的开头、中间和结尾，那么这几个点的试...

六西格玛 中质协考试

赞同0  572浏览  0评论 六六老师 2024-11-01 10:38

文章 区组化会增加实验次数吗？为什么？

底了，没有流量的小伙伴看到这里也够了，为你们省流一波。诶诶诶，点个赞再走呗~~~不差流量的主，我们继续~~详细解析兼不差流量版：我们模拟一个DOE实验，4个连续型数据的因子，2水平，加入3个中心点，1 个区组，1次仿行的全因子试验，得到试验次数如下图所示：最终我们可得到19次实验，其中可以看到基本设计16次，中心点3次即：2^4+3=19那么如果我们加入区组，使得区组变为2，会发生什么呢？试验次数会 增加吗？这里还是2水平，4因子的全因子试验可以看出，加入区组以后，基本设计实验次数还是16，试验次数由19变为22，增加的是新区组的3个中心点2^4+3+3=22所以回到开头的话题，大家心里应该明白了...

六西格玛 中质协考试

赞同0  564浏览  0评论 六六老师 2024-11-05 15:57

文章 多变异图最常见的两个问题：如何制图？怎么分析？

”的数据这个我相信大家都没啥问题，问题在于要理解因子1“设备”被因子2“操作员”嵌套这才是能做出这个图形的成败关键！注意：这里记得要勾选“显示单个数据点”，不勾选直接得出的是2次读数的平均值。勾选后可 以得到2次读数的单个具体值，如下图所示：问题二：图形做出来了，可以看到哪些信息呢？这里的多变异图又是指什么意思？答：可以看到产品内变异、产品间变异、时间变异。①首先，我们看产品内的变异产品内的变异，就 是我用同一个设备做的两个产品，得到两个不同结果的差异如图红色方框所示，明显看到组内差异明显举个例子，比如A用1号设备生产两个产品，从图形上大概得出直径数据8.2和8.4操作员B用2号设备生产两个产品，...

六西格玛 中质协考试

赞同0  698浏览  0评论 六六老师 2024-11-05 16:05

文章 代码化是不是多此一举？

？把原始数据代码化到底是不是多此一举的无用举措呢？带着这些疑问，我们进入：自习人课堂代码化 ，是将该因子所取的低水平设定的代码值取为－1，高水平设定的代码值取为 1，中心水平定为0。举个例子，我们在实 验中温度作为一个因子，我们取高水平100℃，低水平60℃。那么中心点就是80℃。代码化后，我们将高水平100℃变为+1，中心点80℃变为0，低水平60℃变为-1。统计学家通过大量的理论证明代码化后有很 多好处:（1）量纲相同。代码化后的回归方程中，自变量及交互作用项的各系数可以直接比较，系数绝对值大者之效应比系数绝对值小者之效应更重要、更显著。大家知道，对自变量原始数据所进行的回归方程中的回归系数是...

赞同0  578浏览  0评论 六六老师 2024-11-06 09:25

文章 实验设计的三大基本原则你都了解吗？

嗦一句，minitab里的仿行数如果填1，代表什么含义？这里的1，是重复了1次还是没有重复呢？可以看到minitab输出结果：这是一个2因子2水平的全因子试验，加了3个中心点，试验次数是2²+3=7， 仿行数1，有同学就认为重复了一次，但是实际上minitab的逻辑仿行1是没有重复的，仿行2才是重复1次，是不是有点奇怪？这里大家需要理清一个概念，重复是在相同条件下重新做完全重复试验，而不是单纯的去重 复观察或者重复取样。因为同单元重复取样得到的差异估计试验误差将会造成低估，识别不出真实的误差，所得的结论就都是不可信的。（敲黑板：重复可以识别纯误差，可提高效度）我们在试验安排中一定要包含真正的重复，...

六西格玛

赞同0  1152浏览  0评论 六六老师 2024-11-06 09:30

文章 如何策划并分析离散型MSA？一文教会你

过程。与连续型MSA针对的是可以量化测量值（如长度、重量）的情况不同，离散型MSA关注的是分类评价结果的一致性和正确性。它主要涉及以下几个关键方面：1.一致性（Agreement）：不同评价者之间对同 一产品或过程属性判定结果的一致性。这通常通过Kappa统计量或百分比协议来衡量。2. 准确性（Accuracy）：测量结果与实际情况的符合程度，即评价的正确性。可以通过将专家判定作为“真实”结果，与测 试评价进行比较来评估。3. 稳定性（Stability）：长时间内，评价标准或评价者对相同属性的判定保持不变的能力。4. 明确性（Clarity）：评价准则需要足够清晰，确保不同评价者能基于相同的理解...

赞同0  802浏览  0评论 六六老师 2024-11-06 10:10

文章 离散型过程能力分析不会看？一文教会你

全不知道怎么弄今天，我们就一起来做一个离散型数据的过程能力分析，为了保证小伙伴的隐私，我对数据做了一些修改，如下：数据情况说明：2023年1-12月，每个月生产一百多批次产品，不合格品数1代表有1批产 品全部不合格。他跟我说这个的时候，我心里非常沉重，因为在未做分析之前，单凭肉眼看，就知道这个浪费挺大的。我们将数据导入到minitab，路径如下：注意：这里的实际样本量就是每个月的批次数量，一定要录入 实际批次数量，不然会默认每个月批次数量一样。目标默认为0，追求零缺陷嘛，得出如下图形：接下来就需要做图形分析了先看左上图：这是P控制图，由于每个月批次数量不一致，所以出现了凹凸不平的城墙状，这并不是因...

六西格玛

赞同0  623浏览  0评论 六六老师 2024-11-07 09:29

文章 没有minitab，列联表和双比率假设检验该怎么手动计算？

这是2023年中质协六西格玛黑带考试的一道原题，大家在日常工作中遇到这个题，很简单，直接用minitab跑一下就行了第一步，数据分类。将看过广告的总人数，A150人分为记得人数50(OK），不记得人数 100（NG）；B195人分为记得人数75（OK），不记得人数120(NG)。输入minitab：第二步，通过统计-表格-相关性的卡方检验第三步，将OK NG纳入表格，点击统计量，勾选每个单元格的卡方 贡献可以得到卡方值和P值第四步，P=0.326＞0.05，我们可以得出不能拒绝原假设的结论。所以选B那考试的时候，我们没有minitab，怎么得出这个结论呢?没错，我们有两个办法来解决它一方面我们可以...

六西格玛

赞同0  715浏览  0评论 六六老师 2024-11-07 09:45

文章 量具R＆R（方差分析）报告还不会看？安排！

测量系统能力不足。我们总是希望这样，如下图：因为只有量具R＆R，重复性，再现性这三个的变异变小了，部件间的变异才会变大，它们的平方和为100%，也就是合计变异。我们看左中图：左中图是以每个测量员测量同 一个部件的极差形成的R图，数据点绝大多数应该落在控制限之内。本例中虽然所有数据点都落在控制限之内，说明各部件测量结果的极差并无特异者，但此控制限范围太宽，说明重复性误差太大；（敲黑板，画考点）大家记住 哦，重复性好不好是要看这个R图看左下图：左下图是以所有部件的总平均值为中心，以重复观测的标准差为标准差绘制的常规控制图，正常情况应该是绝大多数平均值点落在控制域外，因为越多的数据点超出Xbar图的控制...

六西格玛

赞同0  728浏览  0评论 六六老师 2024-11-08 15:10

文章 量具的不确定度和分辨力

化量。它是量具特性的一部分，表示量具能显示的最小变化。例如，一个刻度为1mm的尺子，其分辨力就是1mm；而一个数字万用表的分辨力可能是0.01V。分辨力反映了量具的精细程度，但并不直接反映测量结果的准 确性或可靠性。区别总结1.定义不确定度：测量结果可能偏离真实值的范围。分辨力：量具能够分辨的最小变化量。2.性质不确定度反映了测量的可靠性和准确性。分辨力反映了量具的精细程度。3.影响因素不确定度受多 种因素影响，包括系统误差和随机误差。分辨力主要由量具的设计和制造决定。4.单位不确定度通常以测量单位表示（如mm、V等），也可以用相对不确定度表示。分辨力是量具的特性，通常以最小刻度或最小单位表示。理...

MSA

赞同0  692浏览  0评论 成都-打杂-王 2024-11-12 22:50

文章 如何做非正态数据的过程能力分析？

方案：第一个方案：通过Box-Cox或者Johnson将非正态数据转换为正态数据Box-Cox转换：（1）估计合适的Lambda（λ）值； （2）计算求出变换后的数据y *； （3）根据原来给定的US L和LSL，计算求出变 换后的USL *和LSL *；（4）对y *用USL *和LSL *求出过程能力指数。Johnson转换：（1）根据Johnson判别原则确定转换方式；（2）计算求出变换后的数 据y *； （3）计算求出变换后的USL *和LSL *； （4）对y *用USL *和LSL *求出过程能力指数。第二个方案：当Box-Cox或者Johnson都不能将数据转换为正态数据，可以用非参...

六西格玛

赞同0  853浏览  0评论 六六老师 2024-11-17 21:55

文章 什么！六西格玛考试也可以勾重点？

别关注。希望能帮助到大家第一章六西格玛管理概论1.1 六西格玛管理的发展1.1.1 质量概念的演进和质量管理的发展1.质量概念的演进质量：一组固有特性满足要求的程度。（ISO9000:2015）（1） 质量概念中主体的演进质量概念中的主体是指“什么的质量”。n产品的质量。包括性能、可信性等实物质量。n产品和服务的质量。扩展到包括准时交付、周期时间等服务质量。n产品、服务和过程的质量。过程质量涉及5M 1E，质量体现Q（实物质量）、C（成本）、D（交付）、E（环境）、S（安全）的综合质量。n产品、服务、过程和体系的质量。体系质量即管理系统的质量。（2）质量概念中客体的演进质量概念中的客体是指“满足什...

六西格玛

赞同0  654浏览  0评论 六六老师 2024-11-17 21:55

文章 中心极限定理到底是什么？它的三个核心要素，你怀疑过吗？

，每组30个数据，标准差为3.3361，根据均值标准差（标准误）=总数据的标准差除以根号下子组样本量=3.3361/根号下30=0.60，和20组数据的均值标准差为0.5697非常接近。这就符合了中心 极限定理的③均值的标准差的公式：彦祖看到这里不禁恍然大悟，原来竟然是这样！赶紧去炒菜去了~~讲到这里，请问下屏幕前的各位彦祖是否曾经也怀疑过中心极限定理？现在是否能深刻体会到中心极限定理的三个核心要素 ？再次回顾一下：①不论之前为什么分布，均值近似正态分布②均值不变③均值的标准差的公式：这是六西格玛考试历年来必考的题目我们再来强化练习一下，加深印象这道题考察的是中心极限定理的三大核心要素在公众号自习...

六西格玛

赞同0  603浏览  0评论 六六老师 2024-11-19 16:20

文章 测量系统MSA线性和偏倚不会分析？2000字教会你

下图所示：我问她是如何策划以及实施的这次量具研究，她给了我这个表格：她分别取了标准重量为2、5、10、15、20kg的大米（用更高精密仪器确定的参考值）用台称测量六次重量得出以上测量值我们都希望测量是 精准无误的，但是实际值测量出来有所偏差如何判断这台秤是否有偏倚，是否有线性呢？第一步先确定是否有偏倚首先我们来看这个图形，横坐标是参考值，纵坐标是在2kg的时候有6个蓝色的点，是偏倚值。我们知道偏倚= 测量值-实际值这些点是台秤去称量得出的实际值减去实际值2kg所得的差值，有正有负。以此类推可以看到5-10-15-20kg时所测量的数据有偏倚值。中间红色正方形的点，则是这6次实际测量值的平均值。但是...

六西格玛

赞同0  662浏览  0评论 六六老师 2024-11-19 16:38

文章 如何用六西格玛QFD质量屋去开一家饭店？

还是第一次听到这个词语，我们有必要复习一下质量屋的基本概念。红皮书510页： QFD（Quality Function Deployment，质量功能展开）质量屋是一种先进的质量管理工具，主要用于产品 开发和设计过程中。为了适应市场竞争，必须以顾客需求为导向进行产品开发。QFD的基本原理就是用 “质量屋” 的形式，量化分析顾客需求与工程措施之间的关系，经数据分析处理后找出对满顾客需求贡献最大的工程措 施，即关键措施，或称关键质量特性，从而指导抓住主要矛盾，开展稳定性优化设计，开发出满足顾客需求的产品。说白了就是满足顾客需求，从而提升顾客满意度QFD质量屋的搭建分为七步：为了大家更好的理解QFD的含...

六西格玛

赞同0  598浏览  0评论 六六老师 2024-11-19 16:50