如何做非正态数据的过程能力分析？

: liuxigema1v1 一对一辅导答疑，助力备考六西格玛

0 人点赞了该文章 · 56 浏览

我们知道，在进行过程能力分析的时候，我们需要明确以下要素:

①确定过程输出特性，明确Y是什么；

②确定过程输出特性的要求，明确上、下限；

③确定抽样方案，抽样尽可能只受到偶然因素的影响，尽可能避免异常因素的影响；

④确定过程是否稳定或具有可预测的分布。

过程能力分析的假设前提，一是输出数据服从正态分布，二是过程应该是稳定或者统计受控的。

说到这里，就有小伙伴问：那如果输出不服从正态分布，就不能做过程能力分析了吗？

当我们发现过程输出不服从正态分布，

第一时间是先分析是否有异常因素导致数据不正态，

如果有异常因素影响，则消除异常因素。

如果没有异常因素的影响，数据仍旧不是正态的，该怎么办？

我们有两个解决方案：

第一个方案：通过Box-Cox或者Johnson将非正态数据转换为正态数据

Box-Cox转换：

（1）估计合适的Lambda（λ）值；

（2）计算求出变换后的数据y *；

（3）根据原来给定的USL和LSL，计算求出变换后的USL *和LSL *；

（4）对y *用USL *和LSL *求出过程能力指数。

Johnson转换：

（1）根据Johnson判别原则确定转换方式；

（2）计算求出变换后的数据y *；

（3）计算求出变换后的USL *和LSL *；

（4）对y *用USL *和LSL *求出过程能力指数。

第二个方案：当Box-Cox或者Johnson都不能将数据转换为正态数据，

可以用非参数计算法。

如何将非正态数据转换为正态数据？转换后的数据上下限会跟着变吗？

带着这些疑问，我们开始数据模拟

首先随机一组非正态数据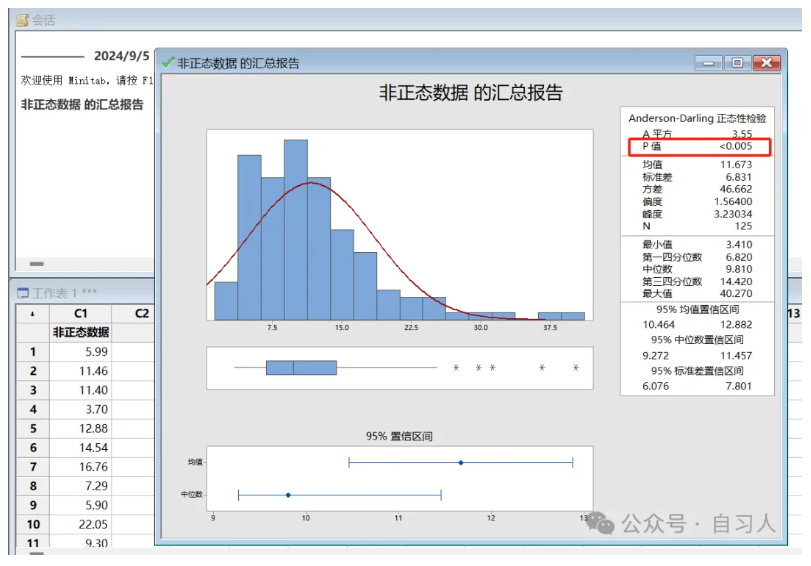

可以看到P值非常小，数据不服从正态分布，并且看图形明显右偏。

我们先用Box-Cox的方法尝试进行转换

minitab路径为统计-控制图-BoxCox变换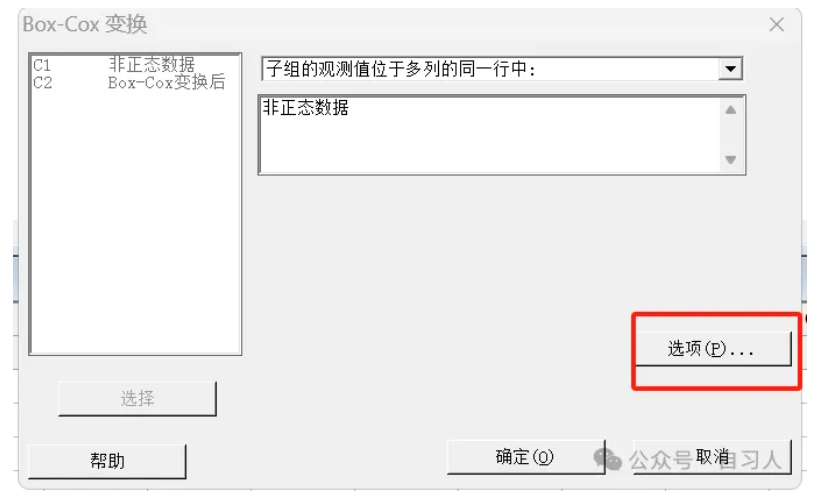

将需要转换的非正态数据放入，然后点击选项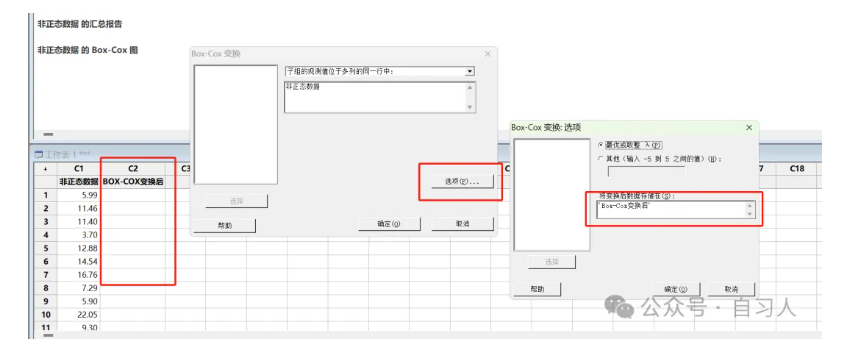

然后将你转换后的数据放入新建的C2那一列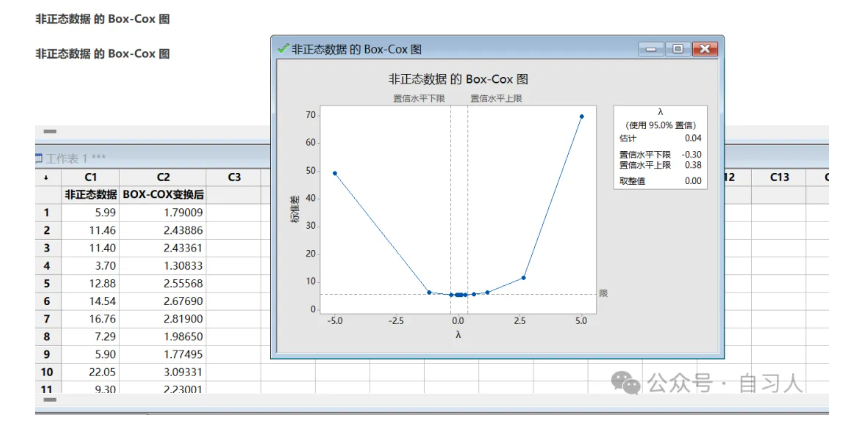

最终得到这个图，可以看到数据变换以后发生了变化，那到底发生了什么样的变化呢？

通过这个图，我们可以看到Lambda的均值有95%的概率落在（-0.30,0.38）之间，系统给到估计值为0.04，为了便于计算，取整值为0。

Lambda取值不同，转换方式也不同，总结如下图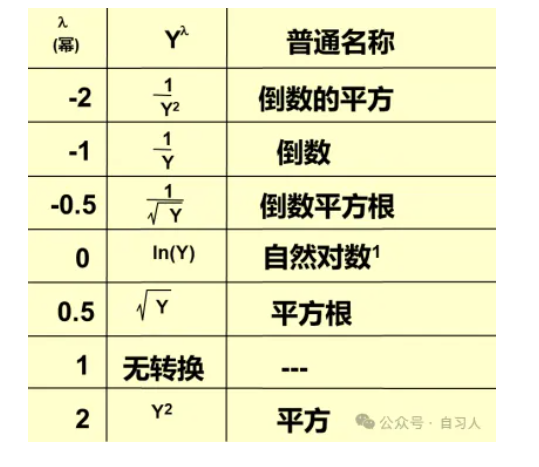

这里取值为0，说明应该取自然对数，

我们来验证一下，将minitab数据复制到Excel，把非正态数据取自然对数，

也就是ln（A），得到的结果和BOX-COX变换后的结果是一致的。

我们对变换后的数据做正态性检验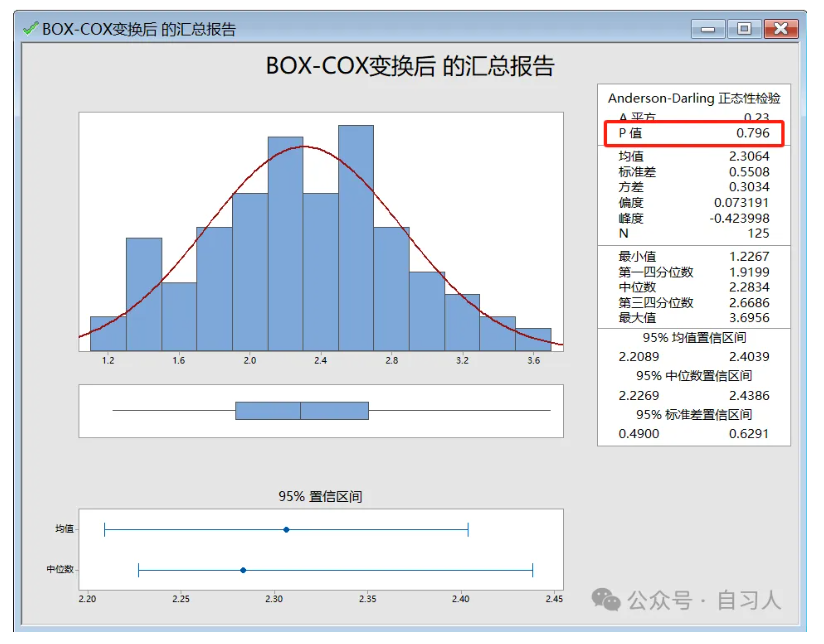

可以看到变换后的数据P值0.796＞0.05，非正态数据变换正态数据，成功！

数据变换以后，下一步我们就要做过程能力分析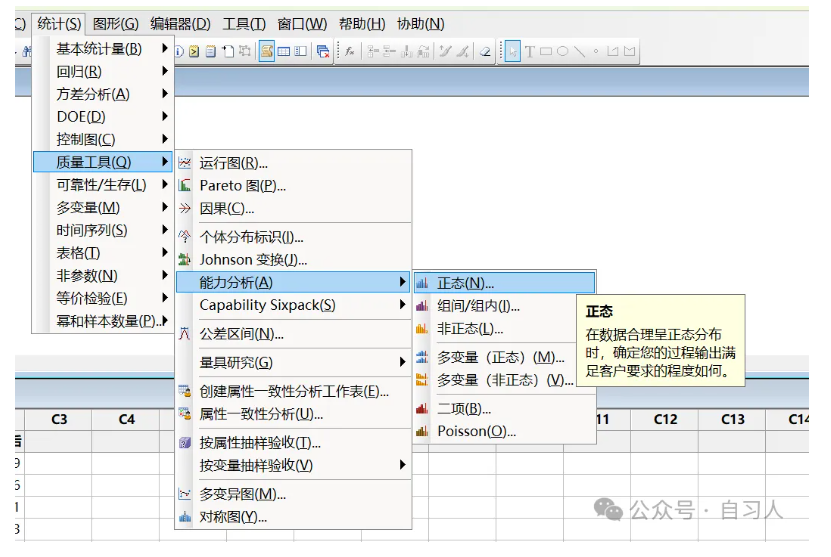

minitab路径为统计-质量工具-能力分析-正态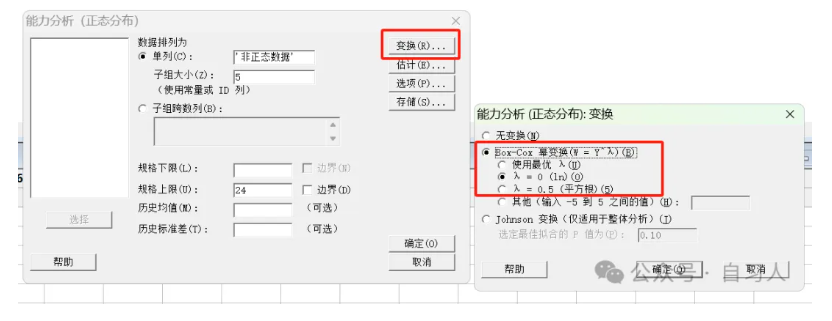

我们将非正态数据放进去，假定子组大小为5，上限假定为24，在变换处选择Box-cox选择Lambda为0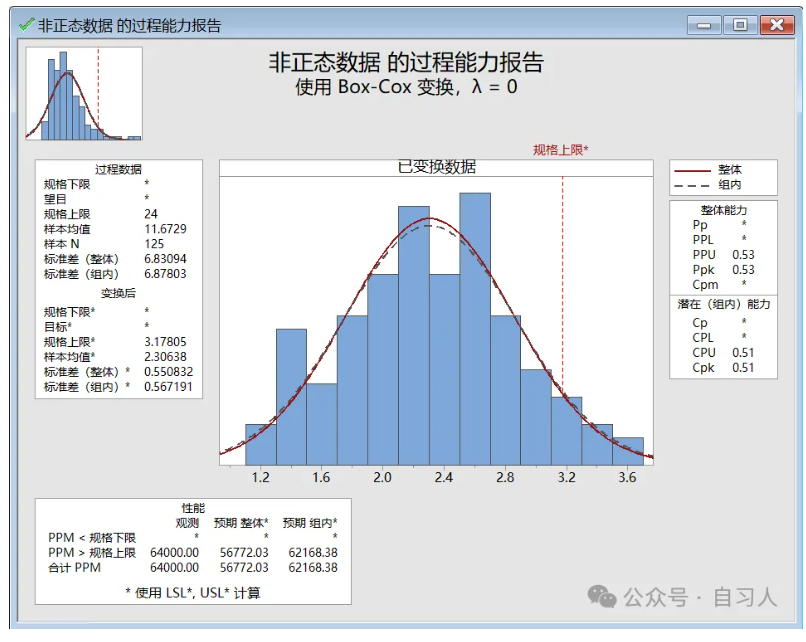

可以得到转换前后的数据分布。得到过程能力指数CPK为0.51.

当然我们也可以直接用转换后的正态数据做过程能力分析，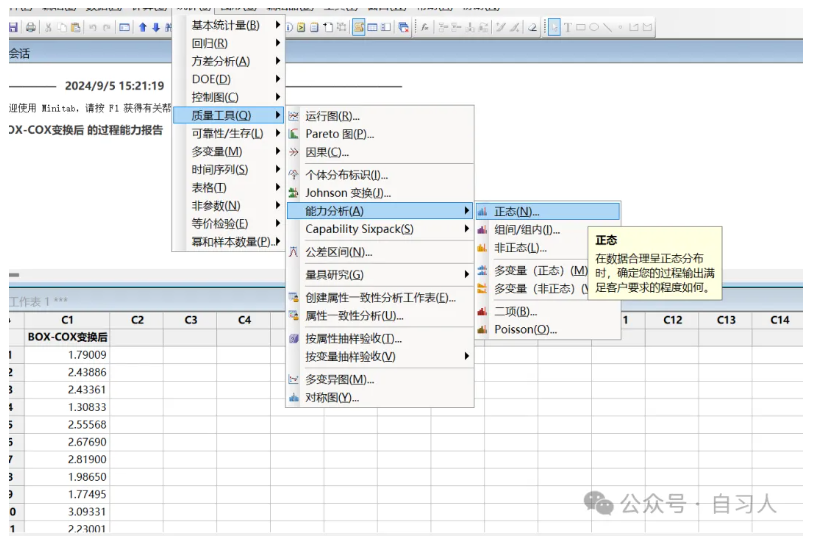

这里需要把上限24转换为Ln24=3.178即可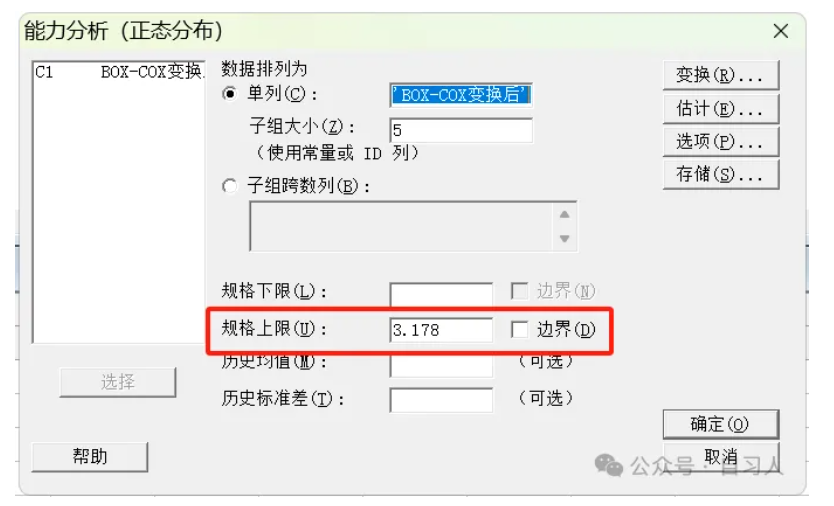

得到如下过程能力分析

得到和之前的过程能力指数一样，CPK为0.51.

我们再用Johnson转换试一下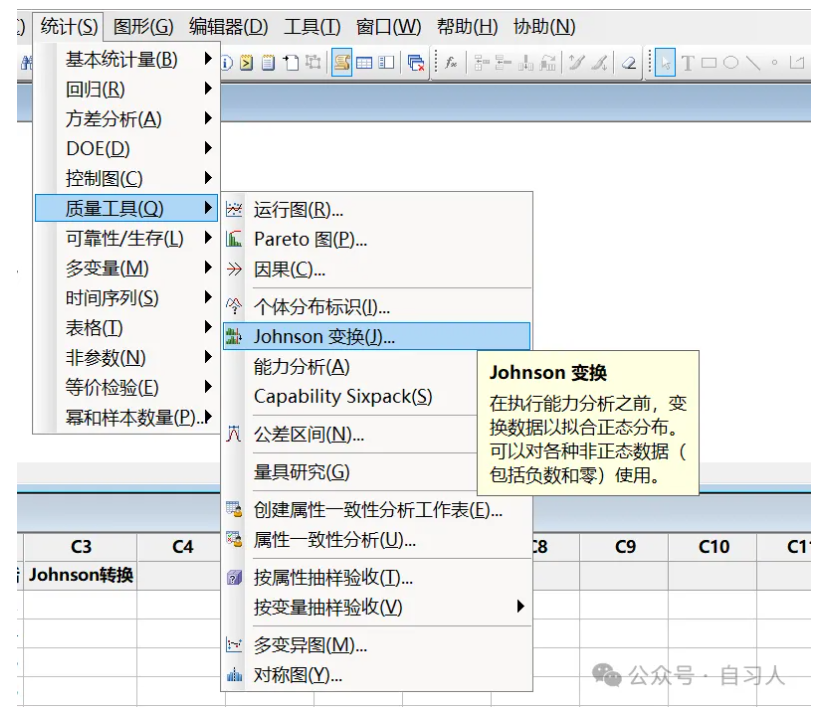

minitab路径为统计-质量工具-Johnson变换

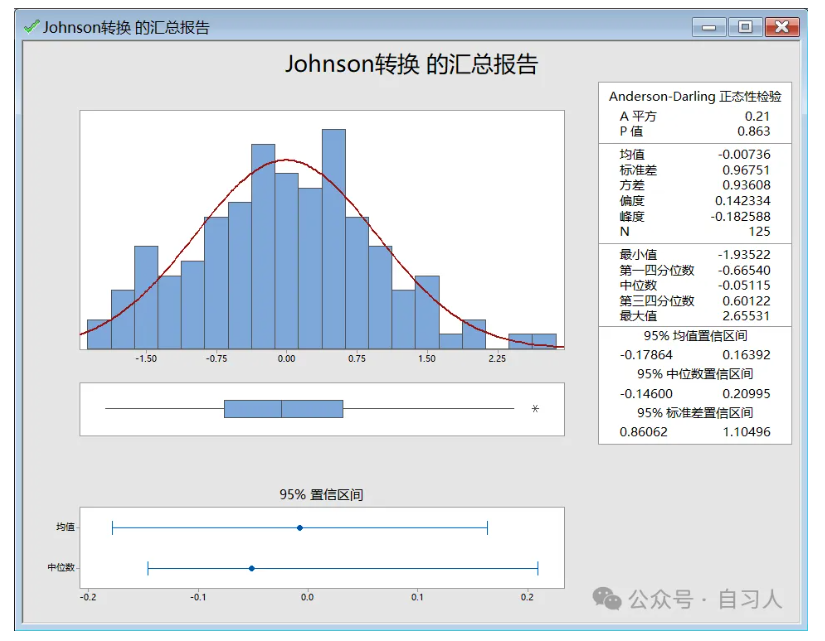
通过Johnson转换后的数据P0.863＞0.05，说明转换后数据为正态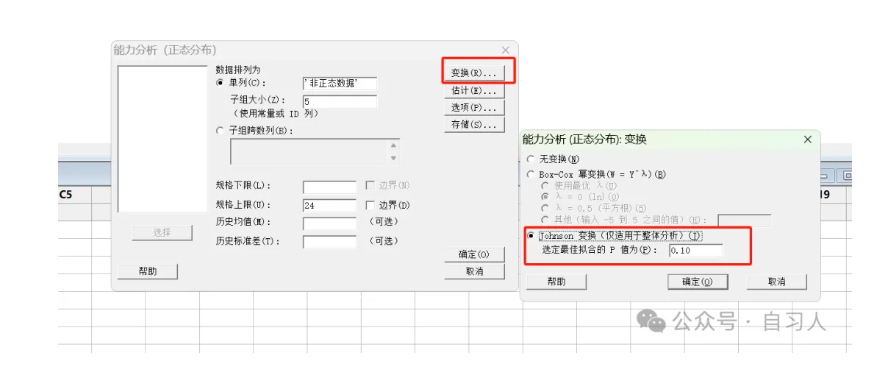

再做过程能力分析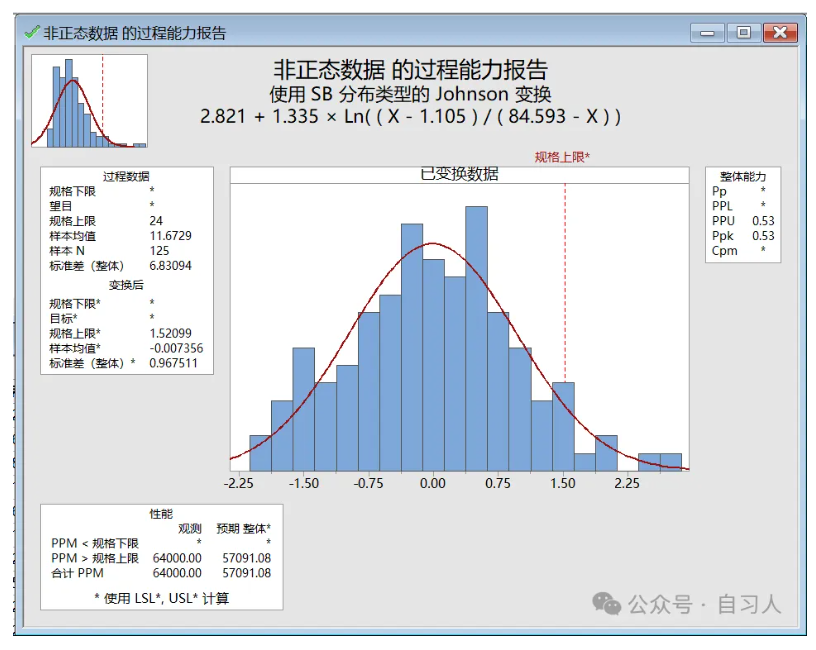

得到PPK为0.53.

说明Johnson变换与Box-cox变换后做过程能力分析，

得到的结论是相差无几的。

在实际工作中，大家学会Box-cox变换足以应对大部分非正态数据的转换了，

如果Box-cox搞不定，再考虑用拟合度更高的Johnson变换。

这个时候肯定有调皮的同学发问：如果Box-cox和Johnson都不能把非正态转换为正态数据，那又如何呢？

答：用Box-Cox和Johnson均无法找到合适的转换方法时，

还有第三种方法可供尝试，即以非参数方法为基础，

不需对原始数据做任何转换，

直接用数学公式就可以进行过程能力指数Cp与Cpk的计算和分析，

这里不作过多阐述。

学习了理论知识，我们再来做题是不是就感觉非常简单了。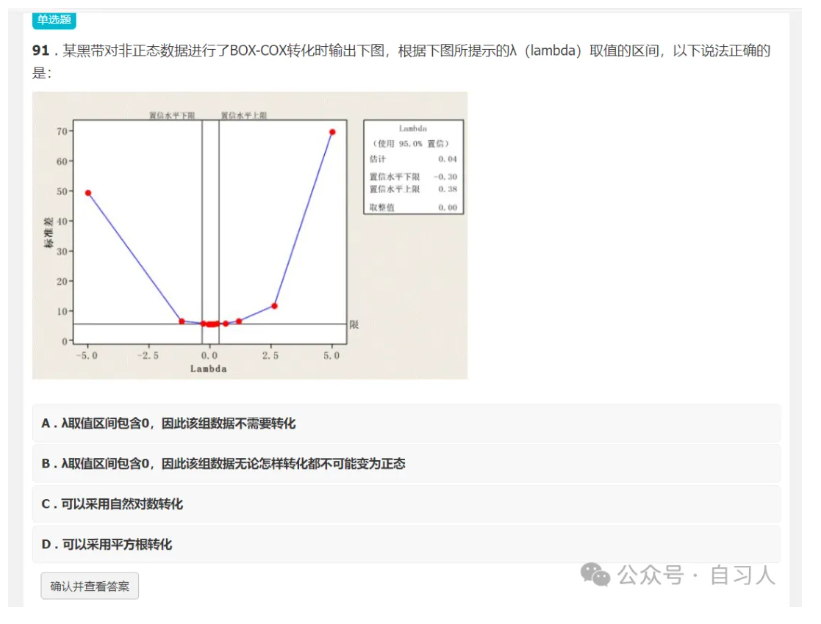

这是公众号：自习人课堂题库里黑带试卷2里的第92题