自习人食堂自开业也来，生意蒸蒸日上，客源不断，一切望好。

前文说到迪丽热酒做了食堂的测量系统MSA线性和偏倚分析，

详情见微信公众号自习人链接：测量系统MSA线性和偏倚不会分析？2000字教会你 

今天，掌勺大厨遇到一个棘手的事情，搞得他心神不宁，局促不安

我看出了他的神情变化，问道：游彦祖，你今天怎么了？

（前台能请迪丽热酒，后台掌勺大厨必须配上游彦祖这个级别）



游彦祖：掌柜的，不好了，大厅来了一位客人，是隔壁老王家的厨师长，

他今天来点了一份“中心极限定理”这道菜，感觉是来砸场子的。

我心中暗道：中心极限定理这道菜，在统计学这个饭圈里它占据了极大的分量。

中心极限定理非常普遍，类似于蛋炒饭，人人都会做，但极少有人能做好，比较考验个人火候。

面对拥有十几年掌勺经验的老王家厨师长，难怪新来的游彦祖如此不自信。

我安慰道：游彦祖，别急，我们来好好梳理下中心极限定理所需材料



游彦祖：这个太复杂了，能否简化得通俗易懂一点？



那我们来总结一下中心极限定理的三个核心要素：

①不论之前是什么分布，均值近似正态分布

②均值不变

③均值的标准差的公式：


游彦祖说这么神奇？不论之前什么分布，它的均值都是正态分布？

我感受到了彦祖的怀疑，非常符合自习人食堂的大胆猜想小心求证！

（咱彦祖可是连定理都敢怀疑的辣个男银！）



于是我们来小心求证一下

我们随机600个自由度为5的卡方分布数据，分为20组，每组30个数据。



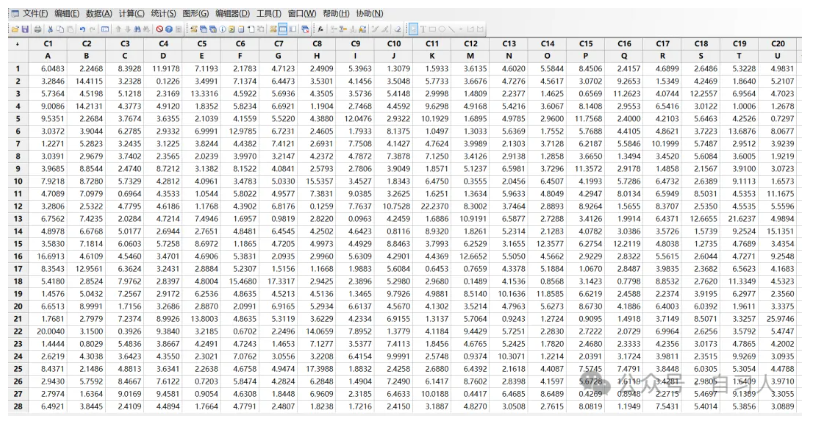
验证600个卡方数据分布是否正态，用概率图


概率图显示P＜0.05，不服从正态分布,

（卡方分布当然不服从正态分布啦！游彦祖小声嘀咕道。）

然后我们将这20组数据求平均值，这个时候复制到Excle表格里计算

（因为minitab只能以列为计算，有时候要结合Excle，便于转置）


再将均值转置到minitab里，做概率图看是否正态


由图形看到卡方均值的概率图P值0.420＞0.05，正态

这就符合了中心极限定理的①不论之前为什么分布，均值近似正态分布

如果感兴趣的小伙伴可以试试指数分布、二项分布、泊松分布也是符合

游彦祖一惊：这也行？那均值不变是什么意思呢？

我们将这600个数据求平均值


得到平均值为4.8988，我们再计算卡方均值的均值


可以看到均值的均值还是等于4.8988

这就符合了中心极限定理的②均值不变



游彦祖又一惊：这也行？那标准误又是什么意思呢？


我们先看这20组数据的均值标准差为0.5697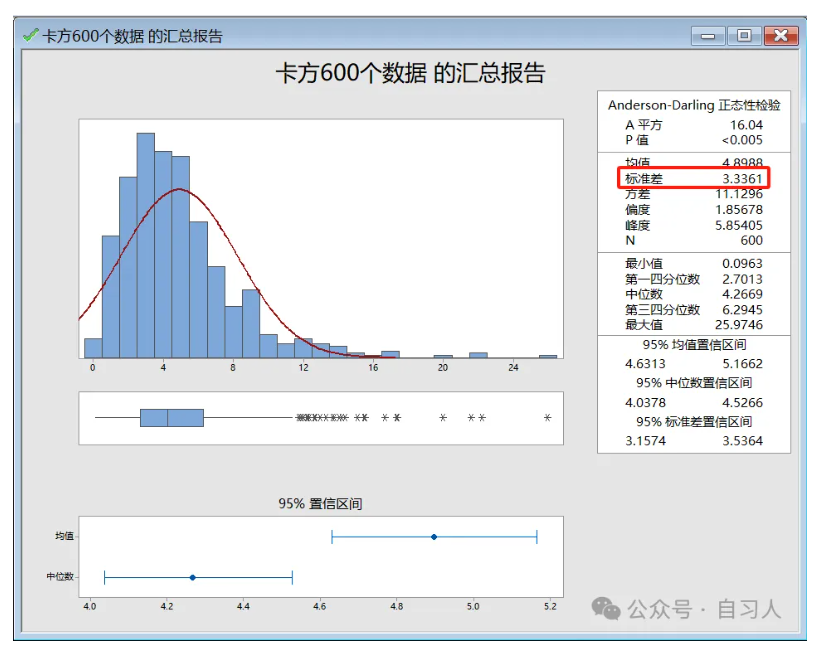

再看总的600个卡方数据分为20个组，每组30个数据，标准差为3.3361，根据


均值标准差（标准误）=总数据的标准差除以根号下子组样本量=3.3361/根号下30=0.60，

和20组数据的均值标准差为0.5697非常接近。

这就符合了中心极限定理的③均值的标准差的公式：


彦祖看到这里不禁恍然大悟，原来竟然是这样！

赶紧去炒菜去了~~




讲到这里，请问下屏幕前的各位彦祖是否曾经也怀疑过中心极限定理？

现在是否能深刻体会到中心极限定理的三个核心要素？

再次回顾一下：

①不论之前为什么分布，均值近似正态分布

②均值不变

③均值的标准差的公式：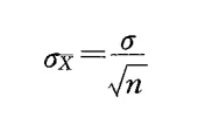


这是六西格玛考试历年来必考的题目



我们再来强化练习一下，加深印象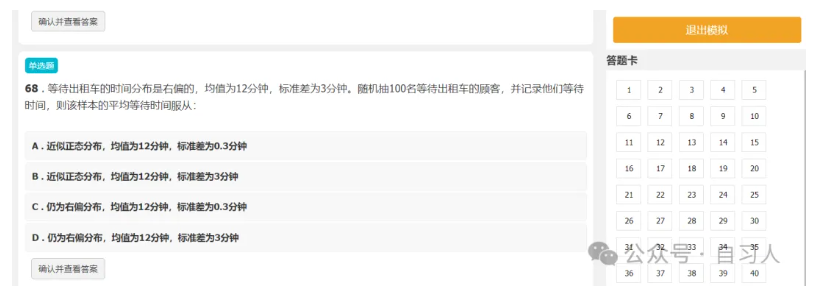


这道题考察的是中心极限定理的三大核心要素


在公众号自习人课堂里的黑带章节练习测量阶段的第68题。答完题以后可以点击图片

每道题都可以查看详细解析

如需帮助，请添加客服时请说明来意

例如：需要相关资料，想进学习交流群，学习计划，备考攻略，项目辅导等