用最通俗的话理解方差分析
针对单个因子而言,方差分析是用来比较多个均值之间是否有显著性差异的有效方法。
若是多个因子,方差分析不仅仅可以比较多个均值之间是否有差异,而且还可以区分出哪些是显著因子,哪些是非显著性因子。
这样说可能有点绕,甚至有点迷糊,下面通过一个例子来理解方差分析。
有四条生产线生产同一个型号的垫片,为了解不同生产线的垫片的断裂强度有无明显差异,现分别从每条生产线随机抽取5个垫片测定其断裂强度,数据如下表所示。
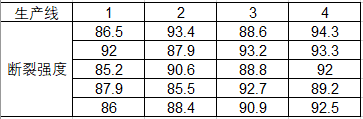
试问四条生产线生产的垫片的平均断裂强度是否相同?
首先,影响断裂强度的因素有两个:生产线、随机因素。
任何一个过程都会有随机因素的影响,即使是同样的生产条件、同一个人操作同一个机器生产同一个产品,也存在随机因素的影响,是无法消除的。
虽然,这种随机因素会导致产品的波动,但影响微乎其微,一般情况下不做处理。在这个例子里,随机因素的影响会导致每一个垫片之间的断裂强度都有差异,随机因素引起的波动用SSE表示。
影响断裂强度波动的另一个因素:生产线,生产线又可以称之为因子。不同的生产线或因子会导致产品的差异,引起产品特性值的波动,这种波动用SSA表示。
这两种因素组合在一起即是过程总的波动,用SST表示。三者是可以进行叠加的,即SST=SSA+SSE
如果SSA>SSE,我们认为因子对断裂强度的影响大于随机因素对断裂强度的影响,因子是显著的。如果SSA≤SSE,我们认为因子对断裂强度的影响不大或不显著。
方差分析的目的就是把过程的总波动分解成不同的子波动,然后比较子波动之间的大小。在方差分析中,总波动SST用总偏差平方和量化,SSA用组间的偏差平方和量化,SSE用组内偏差平方和量化。
总偏差平方和SST意思是每一个数据与总数据的平均值之差的平方的合。
组间偏差平方和SSA意思是每一个水平的平均值与总数据平均值之差的平方的合
组内偏差平方和SSE意思是每一水平下的每个数据减去这一水平下平均值之差的平方和。
是不是更绕了?我们用上面的例子进行验算来理解。
为了便于计算,需要将上述的数据用另一种形式转换,如下:
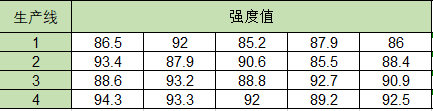
经过Excel的计算,可以得到如下的数据:
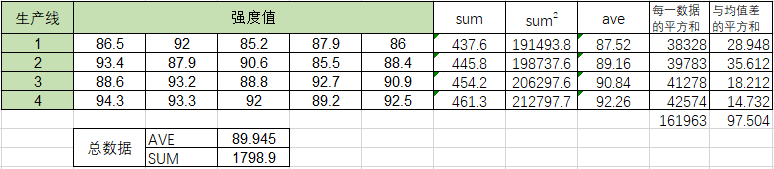
所以:
总偏差平方合SST=(86.5-89.945)*(86.5-89.945)+(92-89.945)*(92-89.945)+……=160.7895,
组间偏差平方合SSA=(87.52-89.945)*(87.52-89.945)+(89.16-89.945)*(89.16-89.945)+……=63.2855
组内偏差平方合SSE=(86.5-87.52)* (86.5-87.52)+(92-87.52)*(92-87.52)……=97.504
这样就把过程的总波动分解成生产线带来的波动与随机因素带来的波动,并进行量化处理。
但是,这里有一个问题。上面量化的三个偏差平方合受数据的多少影响,如果数据越多,则偏差平方合越大。
为了消除因为数据多少的影响,方差分析中引进了自由度分析(自由度的含义不解释)。
我们将组间偏差平方合与相应的自由度之比称之为因子的均方和,用MSa表示。组内偏差平方合与相应的自由度之比称之为随机因素的均方和,用MSe表示。
而当MSa相对于MSe大的多时,这个值超出了拒绝域,则可以认为这个因子是显著的,即每天生产线生产的垫片断裂强度不一样。否则,因子是不显著的,即每条生产线生产的垫片的断裂强度一样。
当然,上面的所有运算都可以在MiniTab完成,仅仅只需要输入一些数据。但是,如果不清楚整个运算过程与方差分析的逻辑,是无法能理解方差分析的含义的。



2021-04-29 20:58