测量系统分析MSA计算再现性:怎么理解“只有一个极差R参与计算,故g=1”?
在测量系统分析MSA这个章节,红皮书上计算再现性波动时,采用的是AV=6σo,其中σo=Ro/d2*
这里d2*需要查表获得,有两个重要的参数:m与g。红皮书上的原话是这样描述的:“因为只有一个极差R参与计算,故g=1,m=k”。
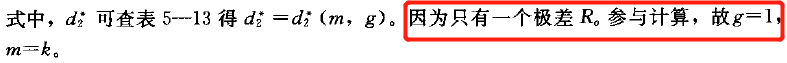
有几个小伙伴对这个描述有些困惑,不太理解其中的意思。
可能有的小伙伴会说,什么年代了,还需要手动计算嘛,直接把数据输入到minitab,然后几个按钮一点,结果就出来了,简直so easy。
我想说的是minitab这一类的软件固然减少了大部分的计算,节省了时间,但其中的含义还是要知道的,有一句老话说的好,叫“知其然,更要知其所以然”,不然测量系统不合格,出现了问题,连原因都不知道,改善的方向更不清晰。我们不可能只会背诵GR&R≤10%是合格的……更要了解其中的含义。
因此,想在这里表述一下,还是以书本上的例子做说明吧。
再现性是指不同的操作者使用相同的量具,对相同零件的同一个位置进行多次测量而产生的波动,主要是衡量由于不同的操作者在测量过程中所产生的波动,用大白话解释就是这种情况下,产生的测量差异只能是由于测量人员不同导致的。
首先,我们先忘记红皮书中的描述,什么只有一个极差R参与计算,先忘却吧。
其次,我们把g当成是子组数量,m当成是子组容量,简单理解就是g表示有多少个子组,m表示在每一个子组里有多少个数据。
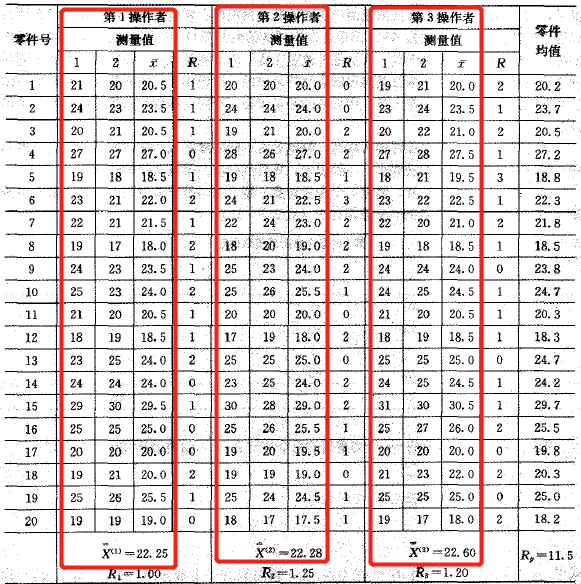
我们再来看原始数据,既然是衡量不同测量人员的差异,就把测量人员测量的零件最终结果当成是一个值,我才不管你测量多少个零件呢,你测10个、20个、100个,你随便,我不管这些,这是你的样本量大小的问题,我只想知道这个样本量里面的样品特征,而均值是表示样品特征的其中一个参数。
那,第1个操作者的均值是X1=22.25,第2个操作者的均值是X1=22.28,第1个操作者的均值是X1=22.60,这3个结果就是这3个测量人员测量出来的样品特征值,而且我们要衡量的也是这3个测量人员的差异。
根据我们刚才说的,把g当成是子组数量,m当成是子组容量。因此,只有一组数据,g=1;这个子组里面有3个数据,m=3,这样参数m与g就知道了,再去查mg表,可以知道d2*=1.91





全部 0条评论