中心点的加入会使得二水平变为三水平吗？

: liuxigema1v1 一对一辅导答疑，助力备考六西格玛

0 人点赞了该文章 · 6 浏览

省流版：不会。

讨论“中心点的加入会使得二水平变为三水平吗？”这个问题之前，

我们就需要首先明确什么是中心点？

为什么要加中心点？

在做试验的时候，我们总是希望不要出现误差，

但是误差总是难以避免的，有什么办法可以估计误差呢？

将每一个试验条件都重复两次或更多次，

这样做的好处是对于试验误差估计得更准确，

但代价却是大大增加了试验次数因而大大增加了试验成本。

这也就是我们常说的重复，也叫仿行。

这样做虽然估计了误差但是增加了试验成本，

对于有的昂贵试验来说无疑是难以承受的。

那有没有什么办法既可以估计纯误差又能最大可能的节约成本呢？

那就是另一种更巧妙的办法只在中心点处安排重复试验，

通常是在中心点重复做三次试验。

这就是我们常说的加入中心点。

重复试验和中心点都可以估计纯误差（这是考点）

加入中心点有以下四大好处：

第一：为了进行完全相同条件下的重复，

因而可以估计出试验误差即随机误差。

举个例子高水平是30g，低水平是10g，

在相同的条件下把中心点20g做三次试验得出数据，

最终得到了中心点这三次的测量值，

就可以计算出纯误差。

第二：由于每个连续因子的取值原来只有两个值(高水平及低水平),

现在增加到了三个值，

因而增加了对于响应变量可能存在的弯曲趋势估计的能力，

这也是简单全面重复所不能达到的效果。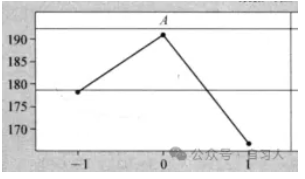

第三：在把因子点试验的顺序随机化之后，

如果再把在中心点处所进行的三次或四次试验安排在

全部试验的开头、中间和结尾，那么这几个点的试验

结果间只应存在随机误差。

如果这几个试验结果呈现非常明显的

上升、下降或其他不正常的趋势，

则有可能帮助我们发现在试验过程中出现的不正常状况。

第四：加上了中心点之后的2水平试验设计在工程实践中已经足够，

在相当大程度上它可以代替3水平的试验，

而且分析简明易行，现已被普遍广泛地使用。

这也是为什么我们学习六西格玛的教材红皮书没怎么过多的解释3水平

因为2水平加入中心点已经能满足日常试验需求。

注意，这里说只是可以代替3水平试验，他本身实际上还是2水平加了中心点而已。

所以回到本文主题，

二水平加入中心点后不会成为三水平，

只是说在某种程度上可以代替三水平！

讲到中心点的知识，

我们不妨回顾一下上期讲的内容，

和这期的串联起来可加深印象

中心点的两个属性类别

①连续型中心点：在所有因子都是连续型变量时容易找到，

那就是各因子皆取其高水平与低水平的平均值。

②离散型的伪中心点：如果因子全部是离散型变量时，

可以选取它们各种搭配中的某一个组合作为伪中心点；

如果因子中既有连续型变量又有离散型变量时，

则可以对连续型变量选取其平均值，离散型变量选取某一个组合作为伪中心点

举个例子：

目前已知有4个因子，3个连续型的因子，1个离散型的因子。

我们知道连续型的因子有中心点，那么离散型的因子如何取中心点呢？

本文的离散型数据是供应商A和B，咱总不能来个（A+B）/2供应商吧

我们可以用连续型的中心点分别去和离散型的两个水平搭配形成伪中心点

这里就不必强行要求实验的平衡，

强调的是确实要有重复。

说白了，就是强行给他加中心点，

并不能算是真正意义上的中心点，所以称之为伪中心点

这里加热温度的中心点7000℃

加热时间中心点15min

均热时间中心点45min

这三个连续型数据的中心点分别去和供应商AB搭配

即，A+7000℃，B+7000℃，

A+15min，B+15min，

A+45min，B+45min，

中心点6就是这么来的。

如果是3个连续型的数据，2个离散的数据，加3个中心点，试验次数又该如何呢？

用刚才教大家伪中心点的逻辑也可以推算出来，

就是用第一个离散型数据的伪中心点6次再去和第二个离散型数据两个水平搭配，

最终形成12个伪中心点。

现在再来给大家分享一个万能公式

实验次数=（2^因子数）*仿行数+中心点个数*（2^类别因子个数）*区组数

同学们可以试着用这个公式再去看看上面这道题，

即：中心点个数*（2^类别因子个数）*区组数=3*2^2*1=12