子组数量大小对过程能力指数cp/cpk的影响
这样一组数据,工程直径6.00±0.02,在尽可能短的时间内连续抽取两个样本,因此,一个子组的数量是2,如下:
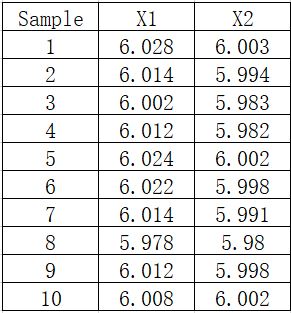
现在不是流行纯手工嘛,先纯手工进行计算,从上面表格里的数据可以知道,X=6.00235,极差均值R=0.0185,容差T=0.04。
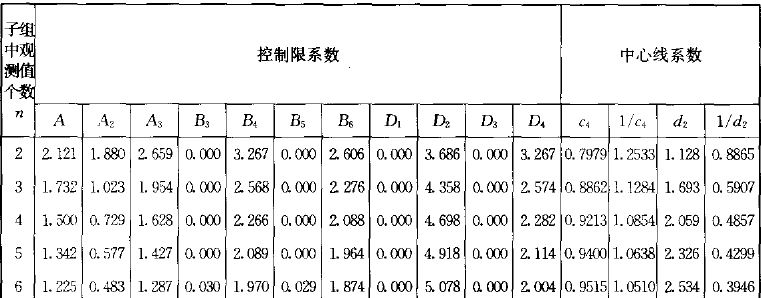
子组数量2,因此d2=1.128
σ=R/d2=0.0185/1.128=0.0164
cp=T/6*σ=0.04/6*0.0164=0.41
cpk=(usl-X)/3*σ=0.35
假如把子组数量增加到5个,在尽可能短的时间内连续抽取5个样本,因此,一个子组的数量是5,形成以下的数据状态,增加的值用x.x表示,这些增加的数值不会影响每个子组极差的变化,也不会引起总均值的变化。
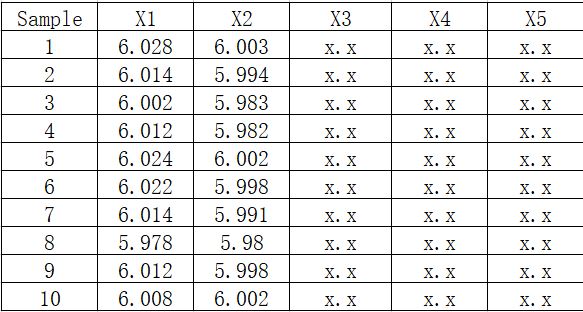
同样,当子组数量是5的时候,计算过程能力指数cp与cpk。
首先,容差是不会改变的,依然是T=0.04,这是在设计之初就已经确定的;
其次,3或6是一个常数,也不会改变,唯一可能改变的是标准差σ。
因为,标准差σ是无偏估计出来的,与极差均值R、系数d2有很大的关系。
前面说了,增加的这些数值不会引起每个子组极差的变化,同样也不会导致总极差均值R改变。
但子组数量变了,系数d2需要改变。
当子组数量是2的时候,d2=1.128
当子组数量是5的时候,d2=2.326
再一次手工计算cp/cpk
σ=R/d2=0.0185/2.326=0.00795
cp=T/6*σ=0.04/6*0.00795=0.84
cpk=(usl-X)/3*σ=0.74
我们把子组数量变更前后的数据放在一起对比:
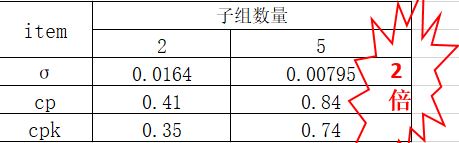
因此,从根本上来讲,子组数量改变影响的是无偏估计出来的标准差σ,从而影响过程能力指数cp/cpk。



2022-04-24 07:52