样本量大于30一定是正态分布,这种说法是真的吗?
经常听人告诉我们:抽样数量大于30个,不需要验证数据的正态性了。
许多人可能默默的接受了这个所谓的“理论”。
但,也有一些不“安分”的小伙伴会追问:“为什么?”
对方语塞。
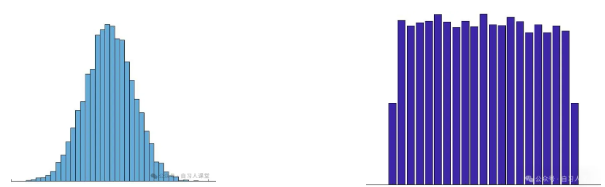
其实,这是一种不正确的说法,也很容易反驳。比如掷色子的点数,你掷30次看看,出现的点数是不是正态分布?
不是的
就算你掷30万次,也不可能是正态分布,而是一种均匀分布。
那么,这种“样本量超过30个是正态分布”的说法来自哪里呢?
有人说这个“说法”来自于中心极限定理。
中心极限定理是一项伟大的发明,经过无数统计学前辈的推演,最终形成了我们现在看到的中心极限定理。可以说,我们是站在前辈们的肩膀上去应用和实践中心极限定理。
中心极限定理是这样说的:
无论随机变量服从何种分布,可能是离散分布,也可能是连续分布,连续分布可能是正态分布,也可能是非正态分布,只要独立同分布随机变量的个数n较大,那么,随机变量之和的分布、随机变量均值X的分布都可近似为正态分布。
而且,为了表述的更加准确,还进一步做了解释:
“当Xi的分布对称时,只要n≥5,那么近似效果就比较理想;当Xi的分布非对称时,要求n值较大,一般n≥30近似效果较理想”
数据30的出处即来源于此。
但是,各位不要只记住了一个数据“30”,从而认定只要样本数量≥30个就是近似正态。
我们不能忽略了该定理中最重要的点:“随机变量之和的分布、随机变量均值X的分布”,这才是核心。
好比你去洗脚,核心是88号技师的业务水平,而不是88号技师的容貌。
有时候,我们总是忽略了本该关注的焦点,而去追求一些“雕虫小技”。
假设检验是六西格玛分析阶段的一个重要内容,是判定有无显著性差异的一个重要工具,比如我们比较熟悉的Z检验、t检验。
正在备考2024年六西格玛考试的小伙伴应该都知道,当总体方差未知,比较均值的时候,要采用t检验。但当是大样本量的时候,可以由样本标准差替代总体标准差,从而弃用t分布,而改用底层逻辑是z分布的z检验。
何为大样本量?
书上标注了一个数值:“30”
因此,有人说“样本量超过30就是正态分布”的依据来源于此。
还是那句话:“我们不能忽略了本该关注的重点”
想一下,t检验是干嘛的?
是检验均值的。
所以,这里的重点仍然是“均值分布”,其实,这里依据的基础理论就是中心极限定理对于一组随机变量之和的分布近似正态。
中心极限定理的应用远不止于此,比如还有Xbar-R控制图。
我们都知道控制图的判异准则是基于正态分布,极差图、c/u以及p/np都是“假定近似正态”才可以使用判异准则,只有Xbar不担心这个,这就是中心极限定理的作用。



全部 0条评论