有人经常说，如果抽取的样本超过30个，样本数据的分布肯定是近似正态的，就不用做正态性检验了。

问其依据或者理论基础来自哪里？

答：中心极限定理

中心极限定理是六西格玛中的一个重要知识点，我们先来回顾一下中心极限定理的内容：

设X1，X2，…Xn是n个独立同分布的随机变量，且有有限的数学期望和方差，分布均值为u，方差u2，则在n较大时，有：

一般情况下，当Xi的分布对称时，只要n≥5，近似效果就比较理想；当Xi分布不对称时，要求n值较大，一般n≥30近似效果较理想。

有人就说，开头的这个问题的理论依据就来自于此。

这样吧，你做一个试验，一个比较有名的试验：“抛色子”，相信许多的小伙伴都非常擅长。

啥？你说你不会？

能不能不要装？做质量要实事求是，KTV里和小公主“哐哐”的摇骰盅，难道不是你？

不要说30次，你就是抛色子300次、3000次，得到的数据分布也不是近似正态。

其实，有这种认识，还是对中心极限定理的理解不对造成的。中心极限定理说的是：“无论随机变量服从何种分布，可能是离散分布，也可能是连续分布，连续分布可能是正态分布，也可能是非正态分布，只要独立同分布随机变量的个数n较大，那么，随机变量之和的分布、随机变量均值的分布都可近似正态分布”

注意了，中心极限定理说的不是随机变量的分布近似正态，而是随机变量的和或均值近似正态分布。

因此，抛多少次色子也不会得到近似正态分布，只有抛色子得到点数的和或均值是近似正态的。

统计学中把均值X的标准差叫均值的标准误，用σx表示：

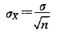
从这个公式上，我们可以知道均值的标准差是随n增大而较小的。

因此，当我们对一个关键质量特性测量时，可以多次测量取平均值，用平均值对质量特性赋值，这样可以减少标准差，让数据更加准确。

中国质量协会每年举行的六西格玛绿带和黑带考试，中心极限定理也是必考的一个知识点。

我们来看一道以前的考试真题：

一位化验员要报告当天每罐氯丙烯产量的平均值。测量3罐后，将其均值Xbar写进报告中，他发现Xbar的标准差（即标准误）为10Kg。如果他希望该Xbar的标准差（即标准误）降为5Kg，问需要测量几罐求平均值？

A.  6
B. 12
C. 18
D. 24

如果知道了标准误σx这个概念，这个题目就很简单了。

σx =σ/√3=10→σ=10*√3

σx=σ/√n =5→n=（100*3）/25=12