控制图连续9点在中心线同一侧为什么判定是异常?
控制图八大判异原则的第2条:“连续9点在中心线同一侧”。这是许多熟悉控制图的小伙伴烂记于心的一个原则,而且很多的资料里面都这样讲,小伙伴们经常掰着手指头在控制图上数数有几个点,有没有超过这个原则。
1.为什么连续9点在中心线同一侧就是异常?为什么?
俗话说:知其然,还要知其所以然,今天来唠叨唠叨。
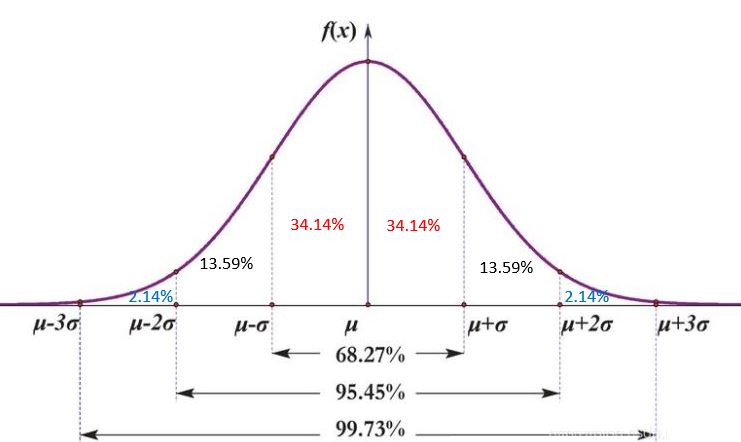
首先,还是要从小概率事件说起,这是基于3σ理论,落在3个σ里面的概率是99.73%,而界外的概率则是0.27%。因此,定义概率<0.27%的事件是小概率事件。
一旦事件发生概率低于这个值,则认为是小概率事件,小概率事件不是那么容易发生,至少在一次试验中绝对不可能发生。一旦出现,则认为是异常。
这是基础理论。
2.“连续9点在中心线同一侧”是什么意思?
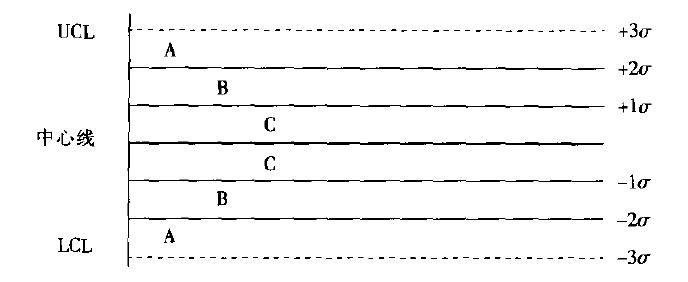
在标准正态分布里,根据σ与中心线,又把±3σ细化成6个区域,即A/B/C,如下图:
一个σ区域定义为C区,两个σ区域定义为B区,三个σ区域定义为A区。“连续9点在中心线同一侧”则是样本观测值连续有9个点落在中心线的上侧或下侧,记住是连续、连续、连续,重要的话说三遍。
3.“连续9点在中心线同一侧”为什么是异常?
这是基于“连续9点在中心线同一侧”的概率与小概率事件发生率0.27%来比较的。我们先计算一下连续9点落在中心线同一侧的概率是多少。
根据上图,可以知道落在中心线上侧或下侧的概率是34.14%+13.59%+2.14%=49.87%
那么,我们先以连续落在中心线上侧计算:
连续8个点落在中心线同一侧的概率:49.87%^8=0.383%>0.27%
连续9个点落在中心线同一侧的概率:49.87%^9=0.191%<0.27%(小概率事件)
连续10个点落在中心线同一侧的概率:49.87%^10=0.095%<0.27%(小概率事件)
连续9点落在中心线上侧的发生率是0.191%,且<0.27%,这样的事件不可能在一次试验中就发生,一旦发生,即意味着有异常,因此在控制图里连续9点落在中心线同一侧被认为是异常的。
同样的计算方法和理论,连续9点落在中心线下侧也是异常的。
各位小伙伴可以根据这个思路理解或计算一下其它6个判异原则中的发生概率。
推荐一个专业的SPC控制图培训资料,下载地址:




全部 0条评论