相信大家对下面这个表格一点都不陌生,没错,你猜对了,这是无偏移状态下的1~6个西格玛的合格率:
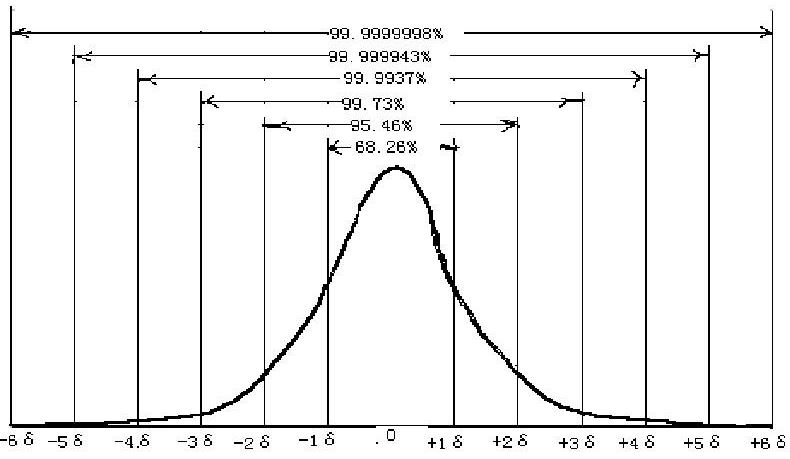
不少小伙伴早已把这几个数值背的滚瓜烂熟,甚至铭记于心,说句不好听的话,结婚纪念日都没有这几个数值记得清楚。
那么,这几个西格玛合格率是怎么来的呢?
有人说查表,当然需要查表,但查表并不能直接看到一西格玛、二西格玛、三西格玛......六西格玛的合格率是多少。
查表肯定是查正态分布表,就是下面这个表格,相信不少的小伙伴看这个表格的频次绝对高于看结婚纪念照的频次。
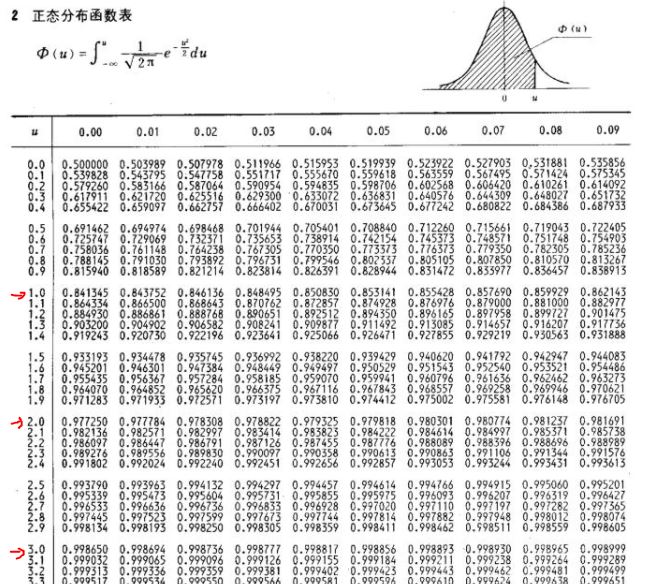
就像上面这个图里面标识的一样,1.0对应的数值是0.84135,即84.135%;2.0对应的数值是0.977250,即97.725%;3.0对应的数值是0.998650,即99.865%。
这和第一张图里的合格率完全不一样啊,哪里出问题了?
正态分布表里对应的1.0是指-∞与1.0之间的面积,并不是一个西格玛的面积,面积就是合格率嘛,概率论老师无数次强调过这一点的,那么一个西格玛的面积怎么算出来呢?概率论老师肯定也教过,只不过被你掺和着老板画的大饼一起吃了。
看下面这张图,我们要求的是-1与1之间的红色面积,即②与③区域
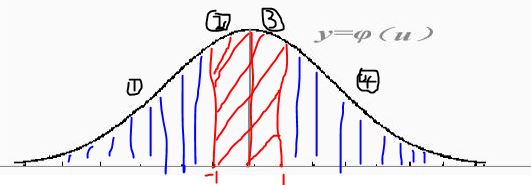
我们查正态分布表知道-∞到1之间的面积,即①+②+③=0.84135
那么红色区域的面积=①+②+③-P(-1)
那么 ①=P(-1) 的面积怎么知道?
由于正态分布的对称关系,①=④
又因为总面积=1
因此,面积①=P(-1)=1-(①+②+③)
那么红色区域的面积=①+②+③-1+(①+②+③)
=2*(①+②+③)-1=0.6827
一个西格玛就算出来了,同理,其它几个数值也可以算出来。
当然,根据正态分布的区间面积公式,可以直接推导出来每一个西格玛的合格率,这里就不一一赘述,有兴趣可以一起探讨。
这几个合格率用的最多的莫过于3个与6个西格玛的,要烂记于心。
参考通用计算方法:https://zixiren.com/article/187.html
我说的不一定对,望独立思考
