双样本t检验与配对数据检验都是检验两个总体均值是否有显著性差异的方法,两者用法千差万别,但又有一些共同点。毕竟,从本质上来讲,配对数据检验只是将数据处理之后再进行单样本t检验。
一.双样本t检验与配对数据检验共同点
1. 样本量来自的总体分布是正态的
2. 两种检验方法只适用于连续型或计量型数据
3. 总体方差未知
4. 适用于小样本量
5. 两者都是比较均值是否有显著性差异
二.双样本t检验与配对数据检验的不同之处
双样本t检验的总体样本是互相独立的,仅仅受测量误差的影响;而配对数据检验的样本除了受测量误差的影响之外,还与样本之间本身的差异有很大的关系。
比如,科学家想比较两种药物对疾病的治愈效果,随机选取了一些人服用药物,选用的这些人之间是互相独立的,但测定的结果除了药物的影响之外,还有选取的这些人的体质之间存在一定的差异,因此不能简单的选用双样本t检验,而是要用配对数据检验。
三.双样本t检验与配对数据检验的实例
接着刚才的话题,随机抽取11个人员,假设药物治愈效果的指标由血糖值来衡量,两种药物在不同的阶段使用,X1与X2代表每种药物服用之后测量的血糖值,如下:
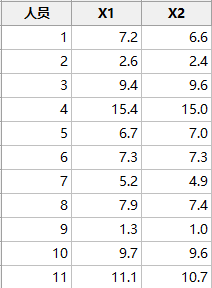
试分析:两种药物的治愈效果是否有差异?
注意:测量值差异如此之大,比如X1的数据从2.6~15.4之间,除了测量误差之外,样本本身的差异对结果的影响更大。
1. 使用双样本t检验
选定显著性水平a=0.05,入口minitab-统计-基本统计-双样本t,分析结果如下:
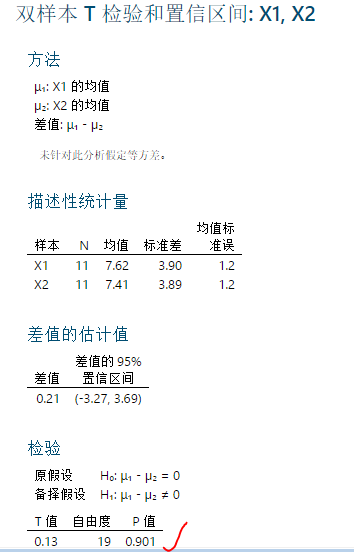
P=0.901>0.05,没有理由拒绝原假设,说明两种药物的治愈效果没有显著性差异。
2. 配对数据检验
配对数据检验考虑了样本之间本身存在的差异,以检验两者的差值△与0之间是否有显著性差异作为假设检验的基础。
这样就转换成了单个正态总体均值是否为0的检验问题。
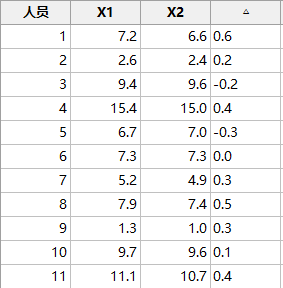
如果△=0,则说明两种药物的治愈效果没有显著性差异;
若△≠0,则说明两种药物的治愈效果有显著性差异。
选定显著性水平a=0.05,入口minitab-统计-基本统计-配对t,分析结果如下:
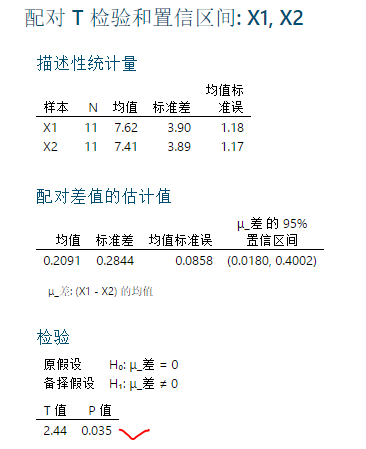
P=0.035<0.05,拒绝原假设,说明两种药物的治愈效果有显著性差异。
由此可见,双样本t检验与配对数据检验的结果是完全不同的,这是因为样本本身存在很大的差异,两组样本的方差都很大,而这种差别又不是由于测量误差导致的,使用双样本t检验很容易得出差异不显著的结论。
因此,在使用双样本t检验的时候,首先要分析样本之间的差异是否足够大,是否受样本本身的影响,否则应该采用配对数据检验。
我说的不一定对,望独立思考
