一般，说样本量是大还是小，通常以n=30为界限，＜30的认为是小样本，＞30的是大样本，这一点在t检验的时候也是这样定义的，久而久之，还形成了一个怪论，认为只要样本量大于30，呈现的分布一定是正态分布，样本量n越大，越近似正态分布。当然，还认为这样说的依据是来源于中心极限定理的概念。

其实，这是理解有误，中心极限定理从来都没有这样表述过，正确的中心极限定理是：“随着样本量的无限增长，无论原来的分布是什么，随机变量X的均值的分布总会趋向于正态分布”。

记住是“X的均值的分布”！！！

为了便于理解，举一个例子：掷色子。

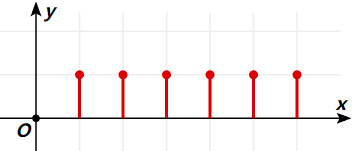
一个色子，点数X是随机变量，出现的结果只会是1-6之间的点数，而且出现的概率是相等的，都是1/6，也就是说不管你掷色子多少次，不要说30次，就是30万次，随机变量X（点数值）的分布也是像下图的均匀分布。

再假设，还是一个色子，掷色子两次，随机变量X是两次色子呈现的点数的平均值，可以想象一下会有多少个数值，以及每个数值出现的概率，如下表：

假如，掷色子30次，或者更多次，这就不是原来的均匀分布，而是近似正态分布了。

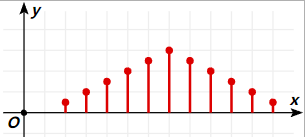
假如，随机变量是掷色子30次的均值，则更加近似正态分布。

所以呢，中心极限定理说的是样本量n的均值呈正态分布，而且n越大，则越近似正态分布。