离散型过程能力分析不会看?一文教会你
今天后台有个小伙伴加我微信,咨询一个问题。
就是如何做离散型数据的过程能力分析?
对于开始做六西格玛项目的同学来说,或许这是一个很简单的操作,
但是对于刚通过考试还没有接触项目的同学来说,
这简直无从下手,完全不知道怎么弄
今天,我们就一起来做一个离散型数据的过程能力分析,为了保证小伙伴的隐私,我对数据做了一些修改,如下: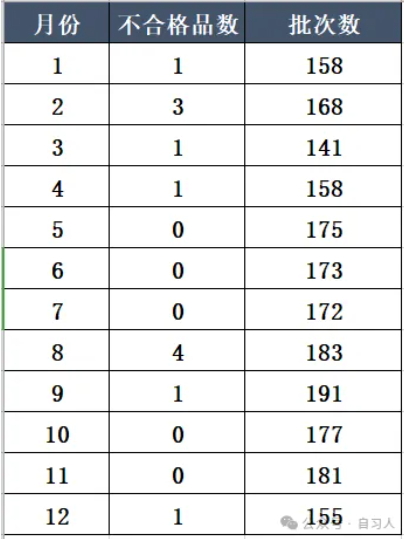
数据情况说明:2023年1-12月,每个月生产一百多批次产品,不合格品数1代表有1批产品全部不合格。
他跟我说这个的时候,我心里非常沉重,
因为在未做分析之前,单凭肉眼看,就知道这个浪费挺大的。
我们将数据导入到minitab,路径如下:

注意:这里的实际样本量就是每个月的批次数量,
一定要录入实际批次数量,不然会默认每个月批次数量一样。
目标默认为0,追求零缺陷嘛,得出如下图形:
接下来就需要做图形分析了
先看左上图:
这是P控制图,由于每个月批次数量不一致,所以出现了凹凸不平的城墙状,
这并不是因为控制图失控了,单纯的只是样本量不一致(考点1),
可以看到每个月的不合格率,在8月份达到了最高,
看原始数据表格得知8月份出现了4次不合格。
绿色的线P-bar是平均不合格率为0.00591,
这里没有%,需要注意识别(考点2),
图中所有的点都在控制线内,说明过程处于统计过程受控状态。
看左下图:
这是累积不良率图,随着时间的推移,
分子叠加,分母叠加,最终呈现如图所示,
这个图最重要的是看%缺陷和Z值。
%缺陷为0.59和左上图的0.00591其实是一个意思,不过是加了百分号
置信区间【0.31,1.03】说明在95%的置信区间下,
缺陷率的均值会落在【0.31,1.03】,
目前均值是0.59(单位都是%)
PPM缺陷为5906,PPM的95%置信区间【3055,10293】
Z值2.5177,Z值的95%置信区间【2.3155,2.7418】
PPM5906是基于Z值2.5177计算出来的,
如果用六西格玛的标准,DPMO=3.4PPM,Z=4.5来衡量,
这个过程能力是比较低的。
看右上图:
这个图表示随着样本量的增大,不良率的呈逐渐下降的趋势(考点3)
右下图:
从图形上直观的看,缺陷率在0附近出现了5次,
0.5%附近出现了5次,
1.0%和1.5%的缺陷率附近没有出现,
缺陷率2%出现了2次。
对照原始表格的缺陷率,吻合。
现在回过头来看这个图形,是不是觉得清晰明了?
在实际做项目分析的时候,这个比较复杂,需要掌握的知识比较多,
但是在六西格玛考试的时候,这个就不难了,我们来试试
我们来做一道2023年也就是去年六西格玛黑带考试的原题: 大家先根据上文所述,
大家先根据上文所述,
自己做一做,
再往下看答案以及解析
公众号:自习人课堂 里的题库每道题是这样,
答题以后可以看答案以及详细解析。
需要相关资料,想进学习交流群,学习计划,备考攻略,项目辅导等扫码添加客服微信




全部 0条评论