引子：

昨天嗓子有点痒，偶尔流点清鼻涕，顿时感觉又感冒了。吃感冒药的间隙，又被父母抓住批了一顿。

“都这么大了还不知道冷热，天变冷了都不知道加衣服吗？”

我反驳道：我本身体质就差，你们都说我从小就爱感冒，是吃药长大的，和穿衣服没啥关系。

父母怒道：“胡说，天冷了加件衣服就不会感冒了”

内心顿时有个疑问：感冒与穿衣服的多少真的有关系吗？君不见凛冽的行风中，有一些人仍然穿着短袖，只要风度不要温度吗？

．．．．．．．．．．．．．．．．

要解决这个疑问，需要用到卡方检验。

卡方检验是分析两种方式或两个因子之间是否独立、是否具有关联性，主要用于离散型随机变量，特别是属性值的数据，比如感冒与穿衣多少。

于是，你带着这个疑问，冒着凛冽的寒风在街头随机取样，并且把穿短袖的认为是穿的少，穿外套的认为是穿的多，随机采访一些小哥哥、小姐姐。

一顿操作之后，你开始整理数据，发现穿衣服多的感冒的有20人，不感冒的130人；穿衣服少的感冒的有49人，不感冒的137人。

按照平时的想法，一顿猛如虎的操作：

穿衣服多的感冒人群比例=20/150=13.3%

穿衣服少的感冒人群比例=49/186=26.3%

此时得出结论：穿衣服少比穿衣服多的容易感冒。

如果学习过六西格玛，你会直接采用更严谨的检验方法：卡方检验

接下来，我们用卡方检验来论证一下刚才的数据，先把数据进行整理，并输入minitab，如下：

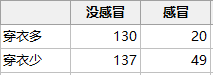
入口统计-表格-相关性的卡方检验，分析结果如下：

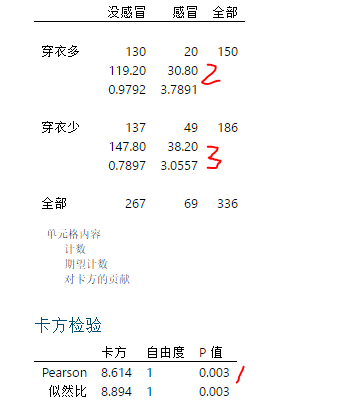
1. 在第一列数据中，从上到下有三个数据，第一行(130)是实际发生的，第二行(119.2)是预计发生的，第三行(0.9792)是方差分量。

2. 卡方检验p=0.003＜0.05，拒绝原假设，说明穿衣多少与感冒有关。

3. 在矩阵图中，方差分量占比最大的是3.7891，穿衣多的感冒的预计人数是30.8，实际发生的只有20人，明显比预计的少很多，说明穿衣多患感冒的人数就少。

穿衣少的患感冒的方差分量是3.0557，居No.2，预计感冒人员38.2，实际发生感冒的人有49，明显比预计的多，说明穿衣少患感冒的人数就多。

这两点与p值的结果是一致的，都说明感冒与穿衣的多少有关联性。可见，真是不听老人言，吃亏在眼前呐。