比较两个均值之间是否有显著性差异，会优先想到使用假设检验，其中比较常用的假设检验有Z检验与t检验。

Z检验或t检验只是简称，全称应该是“两正态总体均值的显著性水平为a的Z检验”或“两正态总体均值的显著性水平为a的t检验”，前面的修饰词很多，但其含义很简单：抽取样本的总体必须是正态分布。

是要求总体服从正态分布，并不是抽取的样本，这是一个比较容易忽视的点。

一．Z检验与t检验的使用区别

Z检验是在总体方差已知的条件下使用，不用考虑样本量的大小，只要总体方差已知，就可以使用Z检验，Z检验统计量与拒绝域如下：

如果总体方差未知，则使用t检验。

与Z检验不同的是，t检验需要考虑抽取的样本量大小，即：大样本与小样本。

大样本是指抽取的样本量数据超过30个，则使用近似Z检验，以计算的样本标准差代替总体标准差，Z检验统计量与拒绝域如下：

小样本是指样本量小于30个，则使用标准的t检验，t检验统计量与拒绝域如下：

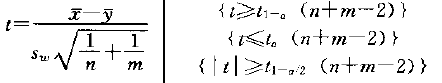
这里有一个点：小样本t检验的前提条件是抽取样本的两个总体的方差相等，即方差齐性。如果不满足这个要求，则不能使用t检验。

因此，在进行t检验之前，我们首先要检验两个总体的方差是否相等。

二．为什么小样本量使用t检验先检验方差相等？

假设有两个总体，X~N(u1,σ1∧2)，Y~N(u2,σ2∧2)，在这两个总体中分别抽取一个小样本，用两个小样本的均值是否有显著性差异去推测两个总体的均值是否有显著性差异。

记住：任何种类的假设检验都是根据样本特征去推断总体特征。

检验两个总体的方差是否相等，其实就是比较总体X的标准差σ1与总体Y的标准差σ2之间是否有显著性差异，即两者数据的离散程度要近似，不然比较就没有任何意义。

比如举重比赛，60公斤级之间互相比赛，80公斤级之间互相比赛，但你选一些60公斤级的选手与一些80公斤级的选手，两者是不能比较的，因为不是一个重量级，各个特征值之间差距较远，即使不比较也能知道。

这就是为什么使用t检验需要先检验方差相等的原因。

三．Z检验为什么不需要先检验方差相等？

这个还真没有找到官方的解释，按照自己的理解简单的说一下吧。

1.     从理论上来讲，Z检验也需要先检验方差相等，但Z检验方差已知，可以直接比较两个总体的方差。

2.     Z检验在计算过程中是转换成标准正态分布，标准正态分布的方差都是1.

如果你觉得这个解释不对，或者有更好的解释，请留言讨论，愿闻其详。

四．案例

从两个总体样本中抽取如下数据，比较两个总体之间是否有显著性差异。

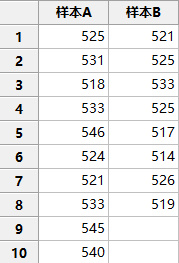
①    总体方差未知，又是小样本量，使用t检验

②    小样本量的t检验需要先检验量总体方差是否相等，即方差齐性，minitab操作如下：

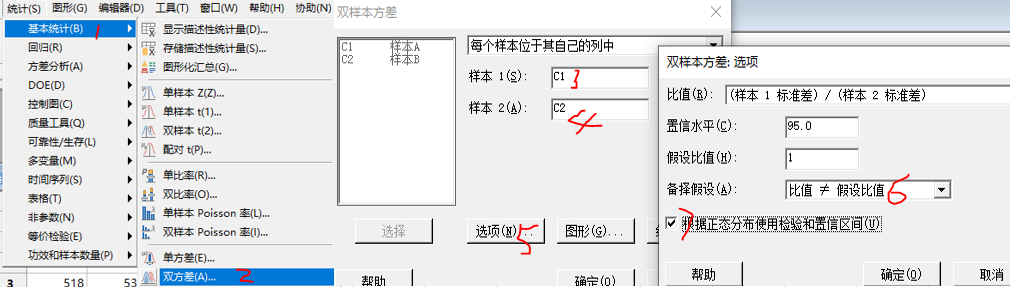
③    方差相等检验结果显示p=0.211＞0.05，无法拒绝原假设，则两个总体方差相等。

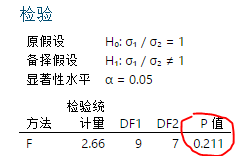
④    确认两个总体的方差相等之后，再使用双样本t检验检验两个总体的均值是否有显著性差异，minitab操作如下：

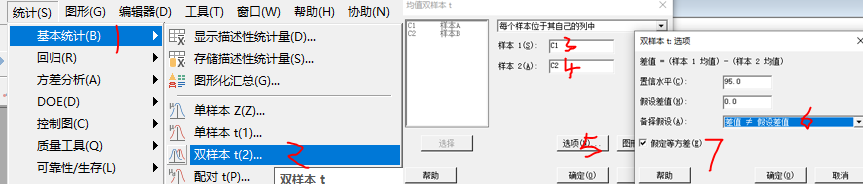
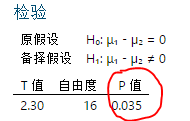
⑤    T检验结果显示p=0.035,＜0.05，拒绝原假设，则两个总体均值之间有显著性差异。

本文“自习人”原创，转载需要注明文章来源：

https://zixiren.com/question/115