一直以来,看到回归方程自变量前面的常数,傻傻的以为是相关系数,其实否也,和相关系数半毛钱的关系都没有。
相关系数是表述自变量与因变量之间是否有关系,以及线性相关的程度。通过散点图只能粗略的知道两者是否有关系,单不知道关系的紧密程度,相关系数则是用一个数值把这层关系进行定量化。
回归方程表述的是自变量与因变量之间有什么样的关系,并通过用方程式的形式直观的表现出来,利用这个公式,还可以预测当自变量变化时因变量的取值。
当人到了一定的年龄,开始发福,啤酒肚开始显现。假如,我们想知道人体内的脂肪含量与年龄是否有关系,随机选了不同年龄的人作为样本,进行测定并对样本数据进行分析。
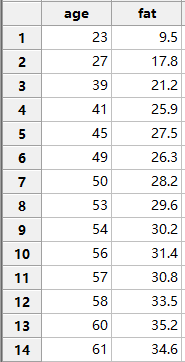
首先,确认两者之间有没有关系,正如刚才所说,两者有没有关系可以通过散点图粗略的知道。
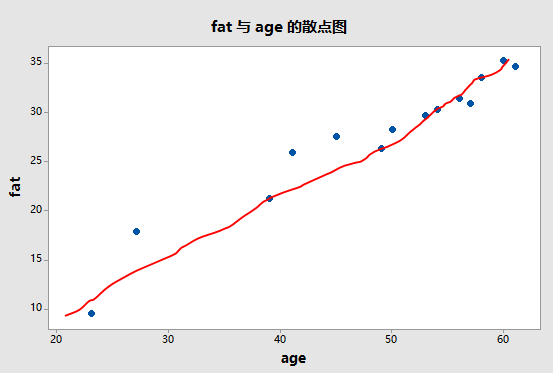
根据散点图,可以看出随着年龄的增长,脂肪含量有一定的增加,说明两者之间是有关系的。
其次,两者的关系到了什么程度?是稍微有点关系?还是密切相关呢?
这个可以通过minitab计算,结果如下:

P=0.000,拒绝原假设,表明脂肪含量与年龄之间确有关系,和散点图的结果相互呼应。
我们知道相关系数r的数值介于-1,1之间,当r=1或-1,两者完全线性相关。此时,相关系数r=0.971,表明两者之间有很强的线性关系。
至此,我们只知道脂肪含量与年龄之间有关系,但究竟是什么关系呢?当随便指定一个年龄,能否大概知道此年龄的脂肪含量呢?
要回答这个问题,需要求助于回归方程,同样用minitab计算,结果如下:
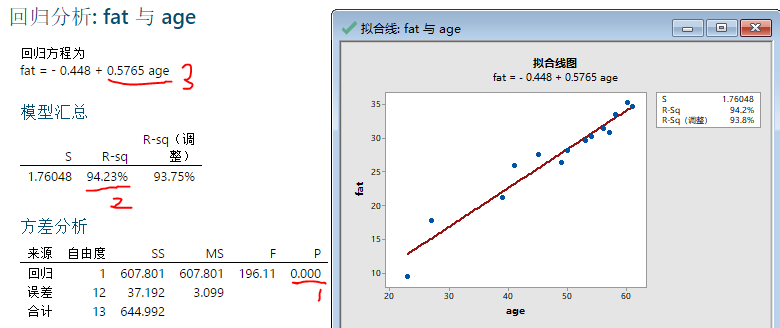
在这里需要注意3个数值:
1. 方差分析表格里的回归p值=0.000<0.05,说明回归方程式显著的,模型是有效的。
2. R-sq=94.23%,称之为可决系数,其含义是回归模型误差占总误差的百分比,是衡量回归方程优劣的一个重要参数,越接近100%,说明回归方程拟合的越好。
3. 回归方程:fat=0.5765*age-0.448,利用这个方程式,我们可以预测任何一个年龄的脂肪含量。
回到文章开头的问题,相关系数与回归方程系数有关系吗?
案例中,相关系数r=0.971,回归系数=0.5765,由此可见两者根本不是一回事。
那么,相关系数r与回归方程之间有关系吗?
当然有。R-sq=94.23%,r=0.971→r∧2=0.971*0.971=0.9428≈R-sq,两者之间有一个推导公式,鉴于太复杂,我不太能理解,只是记住了这个关系存在,有兴趣的小伙伴可以推导一下。
我说的不一定对,望独立思考
