建立回归方程,量化两个变量之间的关系之后,我们需要进行残差分析、诊断以确定拟合的模型是否有效,从而确定是否找到了适用的回归方程。
残差的定义是观测值与因变量的估计值之差,通俗的来讲就是样本试验得到的真实值与通过回归方程预测的y值的差值即是残差。
怎么确定残差是否正常?
在进行minitab确定回归方程的时候,会输出一个残差图,如下:
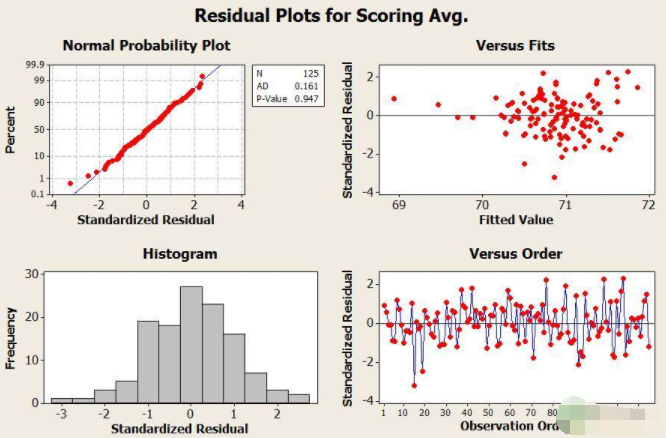
1. 左边两张是残差的正态性检验与残差直方图,残差需要服从正态概率分布。
2. 右上角是回归方程的拟合值与残差图,这个残差图上的点应该分布在一条水平的带子中,不允许有明显的喇叭口。若有,即是提示模型有问题。
上图中出现了明显的喇叭口,则说明残差异常,模型不适用。
3. 右下角是按照观测顺序排列的残差图,回归方程的前提条件是残差均值是0,在这个图上,残差随机上下分布,不允许有异常上升、下降或其它的明显趋势。
除了以上4张残差图,还需要有一个自变量的残差图,横坐标是自变量,纵坐标是残差值,与上图右上角的残差图基本类似。
如果自变量的残差图随机上下分布,则证明说明残差正常,模型适合。
如果自变量的残差图出现异常,比如喇叭口或弯曲,则需要回头再结合上面的右上角的残差图进行分析。
我说的不一定对,望独立思考
