曾经参加一个公司的面试，面试官问了一个问题：在进行假设检验的时候，正常情况下，应该选择样本数量是20个，计算出来的p值是0.049，按照假设检验的判定规则，应该有足够的理由拒绝原假设。但是这一次不小心，作业员比策划样本数量多抽取了10个样品，样本数变成了30个，计算出来的p值还是0.049，这种情况应该是拒绝原假设还是没有足够的理由拒绝原假设？

刚开始有点懵逼，第一反应是面试还带这样问的，第二反应是以前从来没有考虑过这个问题。各位小伙伴，你们考虑过这个问题吗？

我们都知道，在进行假设检验时，需要抽取一定数量的样本。书上为了计算方便，简化了选取样本数量，故而看到的许多案例都是选择10个左右的样本量。但在实际的工作中，样本数量的选择远远不止10个。

对于抽取的样本数量，红皮书上给出了这样的一个公式：

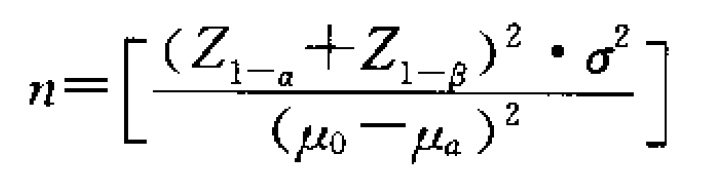
n表示的就是样本数量，从这个公式里，我们能看到样本数量与几个因素有关，比如第一类错误a、第二类错误β、总体方差σ^2，还有前后的均值u0和ua，这5个参数的任何一个发生变化，都会使样本数量改变。

当我们知道了这5个参数，就能很轻松的计算出所需要的样本数量，并且是“从大原则”，什么意思呢？比如说计算出来的样本数量是25.8，那就是需要26个样本；计算出来的样本数量是25.1，也是需要26个样本。简单的说就是升一个数。

这个公式在每年中国质量协会的绿带和黑带考试上也是经常出现，我们来看一道中质协的黑带以前的考试真题：

关于假设检验中显著性水平а和β描述正确的是？

A. 每次抽取的样本量保持不变，增大а值，β也会同时增加

B. 每次抽取的样本量保持不变，增大а值，β会减小

C. 每次抽取的样本量保持不变，增大β值，а会减小

D. β取值一定时，增加每次抽取的样本量，а会减小

在考试现场，如果能记住样本量的计算公式，这个题目就简单多了，比如：

保持每次抽取的样本量不变，增大a值，那1-a值就会变小，Z(1-a)值也会减小，为了保持等式，就要求Z(1-β)值增大，因此1-β就要增大，所以β值就要减小，选项B是正确的。

按照这个思路，C、D也是正确的。

类似这样的六西格玛考试题目解析，网站的六西格玛考试题库里有很多，每一题都有详细解析过程，各位小伙伴先仔细理解，遇到看不懂的我们再交流。

回答刚开始讨论的话题，如果样本数量比策划的数量多，我们是拒绝原假设还是没有足够的理由拒绝原假设？

以单边的假设检验为例子

取a=0.05，计算出来的临界值是1.645，如果样本数量和策划的一样，落在拒绝域就是拒绝原假设，落在承认域就是没有足够的理由拒绝原假设，暂时接受备择假设。

但如果抽取的样本数量大于策划的样本数量，根据统计量的计算公式：

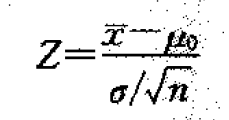
N增大，则Z值增大，就有可能导致检验统计量本是应该落在承认域的，由于样本数量的增加，检验统计量落在了拒绝域，从而拒绝原假设，做出错误的决策。

这句话如果用p值来描述，应该是：由于样本数量的增多，p值减小，就有可能导致检验统计量本是应该落在承认域的，由于样本数量的增加，检验统计量落在了拒绝域，从而拒绝原假设，做出错误的决策。特别是如开头说的状况，计算出来的P值刚好游离在0.05左右的，这样更容易犯错。

那如果所有的公式都记不住怎么办？

这样设想：由于抽取的样本数量增加了，是不是抽取出来坏品的几率增大了？是不是变得更容易拒绝此批产品？其实是一样的道理。