假设检验判定方法:p值、置信区间与临界值有什么不一样?
假设检验的判定结果,总共有3种方法,分别是p值、置信区间与临界值法。
如果看过红皮书,相信都知道如下的假设检验步骤:
1.建立假设
2.选择检验统计量,确定拒绝域的形式
3.确定显著性水平a
4.给出检验统计量的临界值,确定拒绝域与承认域
5.根据样本观察值,计算检验统计量并进行判断。
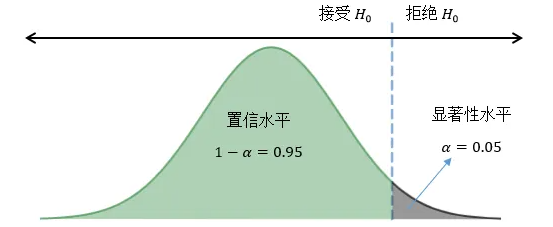
这是一个标准的假设检验的步骤,其中采用的判定方法即是临界值法,也是最早采用的一种手工计算方法,其原理是根据样本计算出检验统计量的观测值,将它与检验统计量的临界值进行比较,观察检验统计量时落在拒绝域还是承认域。
在日常工作中,临界值法已经采用的不多,毕竟现在的软件很方便,已经不需要我们一步步手工计算了,采用更多的是使用minitab,输出结果后分析p值与置信区间。
p值,指的是当原假设成立的时候,由于样本的随机性,出现目前的状况或对原假设不利的状况,即对备择假设更有利状况的概率。

一般取0.05,可以看成是小概率事件发生的临界概率。
当原假设成立的时候,原则上,在一次随机抽样中,抽取的样本特征应该是支持原假设的说法,但恰恰抽取的样本特征不支持原假设的说法,因此我们有理由认为原假设的说法是错误的,从而承认备择假设是真的。
目前的软件在进行假设检验分析时,都会自动计算出p值,不必再手工计算,当然也很难算出,除非搞统计的,一般我们只需要知道怎么根据p值判定就ok。
置信区间法,是根据样本的观测结果去推测总体的置信区间,然后观察置信区间内是否包含了该总体的原假设值。如果原假设值没有包含在置信区间内,则拒绝原假设;反之,则承认原假设为真。
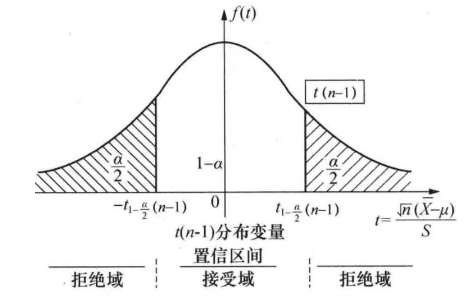
虽然,三种判定方法的出发点不一样,计算过程也不一样,但当给定的显著性水平a一致时,得出的结果应该是一致的,可以说是殊途同归。



全部 0条评论