有人建议,估计总体均值大约取样15个就够了,若是估计标准差则需要取样30个左右,样本的大小直接关系到最终结论的正确性。
简而言之,样本量太小,则样本反应不出总体特征,或者说样本代表不了总体特征,从而做出与真实结果相反的结论。
这种检出真实水平的能力叫检出功效,又叫检出力,用1-β表示。
β是第二类错误的代表符号,意思是当原假设是假,但我们做出了接受原假设的结论。在SPC上,有一个类似的错误,称之为漏报,通俗点讲就是本来是不合格的,结果没有检出来。
因此,β越小,犯第二类错误的概率越小,则1-β数值就越大,说明检出的能力越强,得出的结论更加可信。
除了样本量,检出力1-β还与显著性水平a、总体标准差σ、前后均值差▲X有关系,这几个参数之间有一个公式:
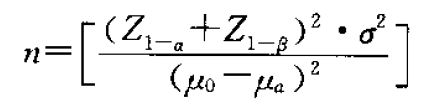
我们找一个案例说明一下

在这个案例种,样本量n=10,显著性水平a=0.05,均值差▲X=0.0058,总体标准差σ=0.015,则计算可以得出Z(1-β)=-0.737
查“标准正态分布的a分位数”表知:1-β=0.23,则β=0.77,犯第二类错误的概率太大了,有很大的概率接受原本错误的原假设,作出错误的结论,这种结论很难让人相信。
如果放在SPC里,则是不良品漏出去的概率很大,这种发货的产品大概率也会有问题。
如果使用minitab计算,则如下图:
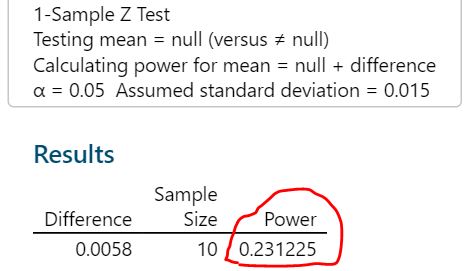
同样得出检出力只有0.23。
那么,如果其它条件不变,只提高样本量呢?
我们把样本量提到10倍,达到100,minitab计算出来的结果如下:

检出力达到了0.97,β=0.03,犯第二类错误的概率大大减小了。当然,β值一般设定在0.1即可,这也是业内认识最常用的一个指标。
因此,样本量越大,则更能反映出总体的特征,更利于我们作出最正确的判断,结论也更容易让人信服。
一般情况下,显著性水平a与β是事先确定好的,我们根据公式计算需要取的样本量即可。
我说的不一定对,望独立思考
