方差分析表是分析因子是否显著的重要工具,读懂方差分析表是最基本的技能。
今天中午,有一个网友问怎么在方差分析表里看是否增加了中心点试验,以及增加了几个中心点试验。
首先,我们知道试验设计的三个原则:重复性、随机性与区组化。
重复试验是试验设计的三个原则之一,目的是估计试验的随机误差。
但是对所有的试验进行重复,成本比较昂贵,试想一个4因子2水平的试验次数是16次,重复一次的话是32次,费时、费钱、费力又伤神。
其次,如果不做重复试验,只增加中心点,能否估计出试验的随机误差?
增加中心点试验无非是比较便捷的一种方法,让中心点试验重复3~4次,并分布在试验的开始、中间与结尾,在相同的试验条件下,这几个中心点试验的结果应该只存在随机误差。
由此可见,如果不做重复试验,只增加中心点,是可以估计出试验的随机误差的。
最后,除了估计随机误差,增加中心点试验有没有别的效果?
当然有,增加中心点试验,相当于增加了一个水平的试验,相当于增加了对响应变量的弯曲趋势的估计能力。
那么,问题来了。
怎么看试验设计是否增加了中心点试验?
下面用两个方差分析表比较一下,两者因子与水平一样,唯一的不同点:一个是增加了中心点,一个是没有增加中心点。
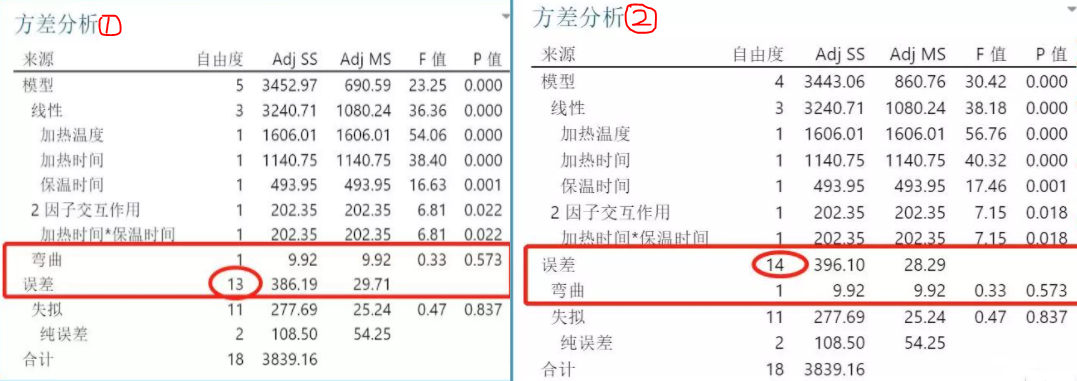
两个方差分析表的最主要区别在于误差项的内容,如下:
方差分析①中:弯曲+误差(包含失拟与纯误差),弯曲不包含在误差里。
方差分析②中:误差(包含弯曲、失拟与纯误差),弯曲包含在误差里。
刚才讲了,增加中心点是可以估计响应变量的弯曲趋势,因此对弯曲的估计需要单独拎出来,所以方差分析①是包含了中心点试验,而方差分析②的弯曲是包含在误差里,并没有增加中心点试验。
那么,怎么知道增加了几次中心点试验呢?
方差分析①里的弯曲自由度是1,因此,中心点试验次数是1+1=2次。
我说的不一定对,望独立思考
