正确的识别随机变量的左偏分布与右偏分布
下面这个图,学习过六西格玛的小伙伴应该不会陌生。
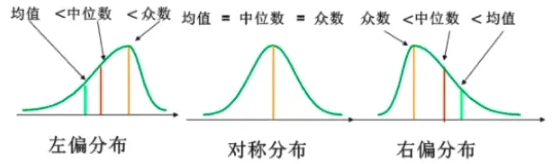
几乎所有的随机变量的分布都离不开这3种类型:对称分布、左偏分布与右偏分布。对称分布很容易记住,不偏不倚、居中呗。其余两个分布却傻傻的分布清楚,经常把左偏当成了右偏,把右偏当成了左偏。
记得当时备考六西格玛黑带考试的时候,为了记住这两个分布,用了一个粗暴简单的办法,最大值往右边扭的是左偏,最大值往左边扭的是右偏,反正是相反的。
说到底,是对左偏分布与右偏分布的概念不理解。
说起左偏分布与右边分布,我们不得不说衡量随机变量分布的特性值都有哪些,比如我们常见的均值与标准差,均值是反应位置状况,标准差是反应离散程度,但只有这两个仍不够完善。
如果能增加反应随机变量分布形状的参数配合均值与标准差,将更能完整的呈现随机变量分布的特性,而偏度与峰度是最常用的两个度量随机变量分布形状的参数。
今天要讨论的左偏与右偏就是随机变量分布偏度的概念。
偏度是对随机变量分布不对称性的度量,计算公式也很简单:

这是计算结果可能会出现几种情况:
1. 偏度=0,记住,偏度=0并不一定是正态对称分布,可能是某一种比较特殊的对称分布。但如果是正态分布对称,偏度一定等于0。
2. 偏度<0,称之为左偏分布,它的分布中低于均值的“尾部”向左侧延伸的特别严重。
3. 偏度>0,称之为右偏分布,它的分布中高于均值的“尾部”向右侧延伸的特别严重。
我们再回头看一下这个图:

因此,我们常说的“偏”并不是“最高点”偏向哪个方向,而是高于或低于均值的尾部往哪个方向偏。



全部 0条评论