通过MiniTab进行单因素方差分析时,输出的结果主要有两个部分:方差分析结果与均值结果。
一.方差分析结果
这是一个比较4条生产线的产品硬度的均值有无显著性差异的方差分析,在这个图上,我们能得到以下几点信息:
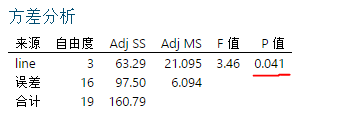
1. 误差的来源有两个:因子line与随机误差,自由度分别是dfA=3与dfE=16。
2. 过程总波动SST=160.79,其中组间偏差平方和SSA因子line=63.29,组内偏差平方和SSE随机误差=97.50,SST=SSA+SSE.
此时的组内SSE>组间SSA,但是这并不代表随机误差是显著性的,因为这两个值受到了因子数的影响,因子越多,数值越大。
3. 是否具有显著性差异是用组间偏差平方和的均方合MSA与组内偏差平方和的均方合MSE比值,其中MSA=SSA/dfA=63.29/3=21.095,MSE=SSE/dfE=97.50/16=6.094.
两者的比值称之为F=21.095/6.094=3.46,观察F值是否落在拒绝域,从而作出判断。
4. p值是整个方差分析结果的精华所在,一般显著性水平a=0.05,若p<0.05,则拒绝原假设,说明均值间有差异;反之,则均值无差异。
二.均值结果
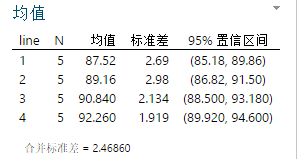
均值结果分析相对比较简单,显示了总体估计的均值与标准差,并给出了置信区间。
一般在选择较优的水平时才使用,比如第4条生产线的预估总体均值最大,我们想要得到较高的硬度值,则选择第4条生产线。反之,则选择第1条生产线。
我说的不一定对,望独立思考
